promien okregu wpisanego Dominik: Długości boków trójkąta prostokątnego tworzą rosnący ciąg arytmetyczny. Wykaż, że jego różnicą jest długość promienia okręgu wpisanego w ten trójkąt. a, b, c − boki trojkata, gdzie c to przeciwprostokatna

⎧	a2 + b2 = c2
⎨	2b = a + c ⇒ c = 2b − a
⎩	r=(a + b − c)2

	4		1
a2 + b2 = 4b2 + a2 − 4ab ⇒ 3b2 − 4ab = 0 ⇒ b(3b − 4a) = 0 ⇒ b =		a = a +		a,
	3		3

	1
czyli roznica jest		a
	3

	4   8   a + a − a + a   3   3		1
r =		=		a
	2		3

cnw i teraz pytanie: czy taki dowod ujdzie? wzoru na promien okregu raczej wyprowadzac nie musze, bo jest w tablicach maturalnych.

Ajtek: Wg mnie jest ok. Tylko zaznacz że a,b,c >0.

Dominik: ze a, b, c > 0 to chyba jasne, bo tworza trojkat, a nie punkt. ale racja, to powinno byc w zalozeniach.

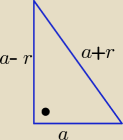
Eta: Można też tak: a>0 i a>r , r −− różnica ciągu arytmetycznego a−r, a, a+r z tw. Pitagorasa (a+r)²= (a−r)²+a² ⇒ a(a−4r)=0 ⇒ a= 4r to boki mają długości : 3r, 4r,5r R −− długość promienia okręgu wpisanego w ten trójkąt

	3r+4r−5r
R=		= r
	2

c.n.u

Dominik: dzieki Eta! bardziej przejrzyste.

Eta: Jeszcze dopisać r>0 bo ciąg rosnący

Ajtek: Eta rozwalasz mnie jak zawsze . Żeby nie było braku kultury, witałem się w tym wątku 185487

Eta: Witam Ajtek