na zbiorach
ssssss: dlaczego w
A=(−2, 3>
B=(−1, 1)
A/B wychodzi nie (−2, 3> ? przecież (−1, 1) należy do B, więc jak w A/B może być w ogóle 1 lub
−1

30 sty 22:01
bezendu: A\B=(−2,−1>∪<1,3>
30 sty 22:06
Mila:
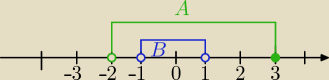
A\B=(−2;−1>∪<1;3>
te punkty zbioru A, które nie należą do zbioru B
30 sty 22:11
Saizou :
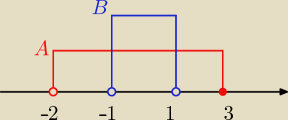
i pytanie co zostanie w zbiorze A jeśli wyciągniemy z niego zbiór B

30 sty 22:12
bezendu:
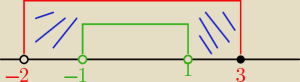
30 sty 22:13
Eta:
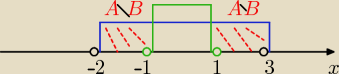
W zakreskowanym zbiorze
−2 jest poza nim czyli... drzwi otwarte a −1 " siedzi" w nim.... czyli drzwi zamknięte
i z drugiej strony 1 siedzi w nim i 3 też siedzi w nim
to:
A\B= (−2, −1> U <1,3>
30 sty 22:16
30 sty 22:16
ssssss: nie rozumiem

jak −2 poza nim, a 3 w nim, skoro oba kółka niezamalowane

30 sty 22:19
bezendu: rozwiązanie jest dobre tylko @Eta się spieszyła i nie zrobiła kółko niezamalowane

popatrz
na rysunki wyżej

30 sty 22:21
bezendu: i zrobiła niezamalowane*
30 sty 22:23
ssssss: jakoś w większości obliczeń w różnicy nie podaje się jakichś "U" i kolejnych dwóch nawiasów.
Wszystko ogranicza się do dwóch pierwszych nawiasów, a nie tak jak wy podajecie − czterech
łącznie.
Czym to jest spowodowane?
bo np, dla A=(1, 3>, B= (−2, 2> raczej by nic takiego nie wyszło"rozbudowanego".
30 sty 22:23
Saizou : Eta używa tzw. metody Bogdana (chyba)

30 sty 22:23
Eta:
Ja kółek nie zamalowuję

Patrzę tylko, które siedzi a które jest poza danym przedziałem
jak siedzi to przedział domknięty a jak poza, to przedział otwarty

30 sty 22:24
Eta:
Dokładnie
Saizou 

30 sty 22:25
ssssss: (−2, 3> nie mogę tak zapisać? zawsze zapisywałem krócej, a tu coś po "U" się dodaje. Tego nie
rozumiem.
30 sty 22:25
bezendu: nie możesz tak zapisać

a to ∪ to znaczy suma przedziałów
30 sty 22:27
ssssss: W rysunku użytkownika bezendu widać, aż za bardzo, że A obejmuje wszystko od −2 do 3 , wiec
chcac nie chcac −1 i 1 zalicza się do A ja tak to rozumiem
30 sty 22:29
Eta:
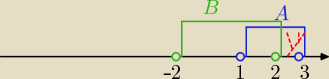 A\B
A\B=(2,3>
30 sty 22:30
ssssss: ze strony pamiętam np. jak jest przedział lewostronnie otwarty, prawostronnie zamknięty (2, 5>
, to zalicza sie 2 i 5 bez 2 . ale nie wiem kiedy sie to uwzglednia a kiedy nie
30 sty 22:31
30 sty 22:33
Mila:

Masz sytuację, że "mniejszy " zbiór jest zawarty w większym i dlatego wycinasz środek a zostaje
Ci kawałek z jednej strony zbioru B i z drugiej.
30 sty 22:34
ssssss: A=(1, 3>
B=<2,4>
i niby A/B = (1,2)
przecież 2 należy do B, zaczyna się od 2 i konczy na 4 , i w dodatku te 2 nawiasy otwarte (1,
2), choć przed 2 jest nawias zamkniety Trudne to

30 sty 22:49
ssssss: tzn miało być B=<2, 4)
30 sty 22:50
bezendu: A\B=(1,2) bo 2 należy do B ale nie należy do A i dlatego nawias jest otwarty
30 sty 22:54

 A\B=(−2;−1>∪<1;3>
te punkty zbioru A, które nie należą do zbioru B
A\B=(−2;−1>∪<1;3>
te punkty zbioru A, które nie należą do zbioru B
 i pytanie co zostanie w zbiorze A jeśli wyciągniemy z niego zbiór B
i pytanie co zostanie w zbiorze A jeśli wyciągniemy z niego zbiór B 

 W zakreskowanym zbiorze
−2 jest poza nim czyli... drzwi otwarte a −1 " siedzi" w nim.... czyli drzwi zamknięte
i z drugiej strony 1 siedzi w nim i 3 też siedzi w nim
to: A\B= (−2, −1> U <1,3>
W zakreskowanym zbiorze
−2 jest poza nim czyli... drzwi otwarte a −1 " siedzi" w nim.... czyli drzwi zamknięte
i z drugiej strony 1 siedzi w nim i 3 też siedzi w nim
to: A\B= (−2, −1> U <1,3>




 jak −2 poza nim, a 3 w nim, skoro oba kółka niezamalowane
jak −2 poza nim, a 3 w nim, skoro oba kółka niezamalowane 
 popatrz
na rysunki wyżej
popatrz
na rysunki wyżej 

 Patrzę tylko, które siedzi a które jest poza danym przedziałem
jak siedzi to przedział domknięty a jak poza, to przedział otwarty
Patrzę tylko, które siedzi a które jest poza danym przedziałem
jak siedzi to przedział domknięty a jak poza, to przedział otwarty



 a to ∪ to znaczy suma przedziałów
a to ∪ to znaczy suma przedziałów
 A\B=(2,3>
A\B=(2,3>
 bo nie znasz wgl teorii
bo nie znasz wgl teorii
 Masz sytuację, że "mniejszy " zbiór jest zawarty w większym i dlatego wycinasz środek a zostaje
Ci kawałek z jednej strony zbioru B i z drugiej.
Masz sytuację, że "mniejszy " zbiór jest zawarty w większym i dlatego wycinasz środek a zostaje
Ci kawałek z jednej strony zbioru B i z drugiej.
