Rozwiąż nierówności, a zbiór rozwiązań przedstaw na osi liczbowej. Buka: Rozwiąż nierówności, a zbiór rozwiązań przedstaw na osi liczbowej. Może mi ktoś wytłumaczyć jak to rozwiązać. Mam jeszcze jedno podobne zadanie ale brak mi pomysłów jak się za to zabrać. x³+2x²−13x+10>0

PuRXUTM: kojarzysz schemat Hornera ?

Buka: Nie kojarzę. O co w nim mniej więcej chodzi?

PuRXUTM: a Ty masz matmę podstawową czy rozszerzoną ?

Buka: Powiedzmy tak. Rozwiązuje od kilku dni mojemu bratu który siedzi za granicą na zaliczenie testy zaliczające do ogólniaka dla dorosłych. Sam szkołę kończyłem dość dawno. Zaliczyłem podstawową matmę w technikum ekonomicznym

PuRXUTM: https://matematykaszkolna.pl/strona/1401.html to brat na pewno będzie umiał... Dzięki schematowi Hornera można rozłożyć wielomian na prostsze czynniki jeśli się da oczywiście. Zaraz spróbuje to policzyć, a Ty przeglądnij sobie tę stronę

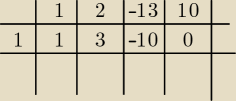
PuRXUTM: x³+2x²−13x+10=(x−1)(x²+3x−10)=(x−1)(x+5)(x−2) − to można z delty albo "na oko" ciąg dalszy w następnym poście bo tutaj nie narysuje wszystkiego

Buka: od razu to lepiej wygląda. mam tylko pytanie. W tekscie pisze że dzielimy przez dwumian "x−c". Skąd bierze się to "c"?

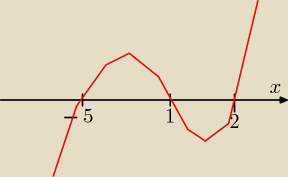
PuRXUTM: (x−1)(x+5)(x−2)>0 Mz: x₁=1, x₂=−5, x₃=2 a₃>0 a₃=1 (x−1)(x+5)(x−2)>0 dla x∊(−5;1) U (2;+∞) i to jeszcze zaznaczyć na osi ( następny post )

PuRXUTM: Buka bardzo dobre pytanie widzę że dobrze to przejrzałeś c to podzielniki wyrazu wolnego czyli w tym przypadku u nas 10 10 dzieli się przez 1,−1,2,−2,5,−5,10,−10 i w schemacie Hornera sprawdzasz po kolei te podzielniki aż na końcu wyjdzie 0

Buka: Ahaaa. Czyli już wszystko rozumiem. Sprubuje sam to ogarnąć. Dziękuje za poświęcony czas. Pozdrawiam

PuRXUTM: Cała przyjemność po mojej stronie