czy mogły ktos mi pomoc z tym zadaniu:)
abuzabi: wykaz ze suma odleglosci dowolnego punktu P od czworościanu foremnego wewnatrz którego lezy
punkt jest równa długosci wysokosci tego czworoscianu
22 sty 18:27
abuzabi: prosze pomocy:(sam nie dam rady
23 sty 17:00
abuzabi: prosze pomoc
23 sty 17:04
abuzabi: POmocy prosze!
23 sty 17:12
23 sty 17:14
pigor: ... , np. tak
niech H
1, H
2,H
3,H
4 − odległości dowolnego punktu P od ścian
czworościanu, a H, S − długość wysokości i pole powierzchni
ściany czworościanu foremnego odpowiednio, to suma objętości
V
1+V
2+V
3+V
4= V ⇔
13SH
1+
13SH
2+
13SH
3+
13SH
4=
13SH ⇔
⇔
13S(H
1+H
2+H
3+H
4)=
13SH / :
13S ⇔
H1+H2+H3+H4= H , a to
należało wykazać . ...
23 sty 17:15
abuzabi: i to jest na pewno to zadanie?
23 sty 17:16
23 sty 17:16
pigor: ... Oj
czuję , że popełniłem ...
przestępstwo edukacyjne, bo zbyt wylewnie mi
dziękujesz .
23 sty 17:20
abuzabi: Nie
poprostu od wczoraj próboje rozwiazac taklie zadanie i nie moge i wgl całe dnie robiłem je
i nic
i dlatego zwróciłem sie o pomoc
Dzieki wam bede mogł je zrozumiec
23 sty 17:22
Mila: Na pewno.
Spróbuję Ci cos narysować, gdy dalej nie będziesz tego "widział".
Pomyśl nad tym co napisał Pigor.
23 sty 17:25
abuzabi: ok
23 sty 17:29
abuzabi: mila narysujesz mi ten rysunek
23 sty 17:47
Mila:
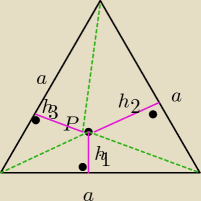
To możesz zrozumieć lepiej na podstawie analogii z Δ równobocznym.
h− wysokość Δ
P punkt wewnątrz Δ
h
1; h
2; h
3 − odległości punktu p od boków Δ
| 1 | | 1 | | 1 | | 1 | |
| a*h= |
| a*h1+ |
| a*h2+ |
| a*h3 /*2 równoważność pól |
| 2 | | 2 | | 2 | | 2 | |
ah=a*h
1+a*h
2+U{1}a*h
3 /:a
h=h
1+a+h
3
23 sty 17:58
abuzabi: no fakt tak bez rysunku by bylo ciezko
DZIEKI
23 sty 17:59
Mila: powinno być:
ah=ah1+ah2+ah3 /:a
h=h1+h2+h3
23 sty 18:00
23 sty 18:01