pola figur
Ada: Proszę o pomoc.
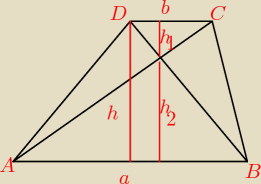
Pola trójkątów, których podstawami są podstawy trapezu, a wspólnym
wierzchołkiem jest punkt przecięcia sie przekątnych tego trapezu, wynoszą P1 i P2. Oblicz pole
trapezu.
3 cze 17:11
Basia: Pomagam
3 cze 17:25
Basia:
Mam gościa. Skończę potem.
3 cze 17:31
Ada: z góry dziękuję
3 cze 17:47
Ada: Jest może ktoś kto by mi pomógł teraz
bo niedługo będę musiała zejść z kompa
3 cze 20:46
Bogdan:
Podam końcowy wynik:
Pole trapezu P = (√P1 + √P2)2
3 cze 20:50
Ada: Basiu, jesteś może ?
4 cze 20:37
Andrzej: Zajrzyj do
17970 to bardzo podobne zadanie.
4 cze 20:42
aska: andrzej bogdan spojrzycie na zadanie moje te 2 co sa na przodzie forum?
4 cze 20:43
Ada: kurcze, mi wychidzu 3P1 + P2
wiec pewnie coś złe robie
4 cze 21:09
Basia:
| | P2 | |
△AOB ~ △DOC w skali k = √ |
| |
| | P1 | |
można przyjąć wobec tego:
CS = x i AS=kx
DS = y i BS=ky
P
2= P
ASB =
12*AS*CS*sinα =
12*kx*ky*sinα =
12k
2*x*y*sinα
P
1= P
CSD =
12*CS*DS*sinα=
12*x*y*sinα
P
ASD =
12*AS*SD*sin(180−α) =
12*kx*y*sinα
P
BSC =
12*BS*CS*sin(180−α) =
12*ky*x*sinα
P
ASD=P{BSC} = P
3
P
1*P
2 =
14k
2*x
2*y
2*sin
2α
P
ASD*P
BSC =
14*k
2*x
2*y
2*sin
α
P
ASD*P
BSC = P
1*P
2
P
32 = P
1*P
2
P
3 =
√P1*P2
P
t = P
1+P
2 + 2*P
3
P
t = P
1+2
√P1*P2 + P
2 = (
√P1+
√P2)
2
4 cze 21:49
Ada: tam w pierwszej linijce to jest pierwiastek z p2 przez p1 ?
dziękuje bardzo
4 cze 21:53
Ada: i czy O i S to ten sam punkt ?
4 cze 22:01