pytanie tn: Witam, W jaki sposób należy opisywać Omegę, Zdarzenia? Czy jest to aż takie istotne? Może symbole, słownie ? Czego się wystrzegać? Jakiego sposobu, może jakieś częste błędy, niedomówienia?

PW: Nie tyle istotne, co ma zasadnicze znaczenie, bez tego ani rusz. W większości zadania szkolne polegają na zastosowaniu tzw. klasycznej definicji prawdopodobieństwa:

	k
P(A) =		,
	n

gdzie k oznacza liczbę zdarzeń wchodzących w skład A (powiadają: sprzyjających A), zaś n to liczba wszystkich możliwych zdarzeń elementarnych. Jak więc rozwiązać zadanie nie wiedząc jaka jest liczba n? Dopiero po uświadomieniu sobie z jakich (a więc ilu) zdarzeń elementarnych składa się Ω, możesz zacząć myśleć o "zdarzeniach sprzyjających zdarzeniu A". Symbole bardzo dobre, ale dla ucznia kłopotliwe. najlepiej opisać słowami, używając terminów matematycznych, np. zdarzenia elementarne to wszystkie możliwe kombinacje (to już zależy od konkretnej sytuacji). Wystrzegać się rysowania drzewek (najskuteczniejszy sposób do ogłupienia, na zasadzie "tak to się robi"). Dawaj konkretne zadania, będziemy pokazywć niuanse.

tn: Drzewek nie używalem do dnia dziś. Nie są takie złe z punktu widzenia mojego. Są one narzędziem, którym umiejętnie władając rozwalę sporo zadan. Jak niby mam sobie radzić z zadaniami z wieloetapowymi zdarzeniami, które od siebie zależą? Np. OKE POZNAŃ STYCZEŃ 2013

Mateusz: Warto zauwazyc ze tzw reguła sum i reguła iloczynu ktorą sie stosuje w drzewkach wynika odpowiednio ze wzoru na prawdopodobieństwo iloczynu i prawdopodobieństwa całkowitego i radziłbym najpierw opanowac te podstawy i potem zajmowac sie krzaczkami ja to traktowałem jako odstresowujące do takich zadań (mozna było sobie pobazgrac na kartce).

tn: Tak, ale przecież całkowitego nie może być na maturze R

Mateusz: Jak nie moze?

Mateusz: Aha i jak powaznie myslisz o matematyce tzn jakis kierunek z tym związany to nie ograniczaj sie do wymogow maturalnych.

Mateusz: A na maturze rozwiązanie poprawne kazdą metodą jest uznawane(nawet całkami)

tn: Tak ja rozumie, ale rzuć okiem tutaj: https://matematykaszkolna.pl/strona/3426.html No więc?

PW: To co pisze Mateusz pokazuje, że przy dobrym rozumieniu sensu zadania "drzewko" może być dobrą ilustracją zastosowanego twierdzenia, ale nigdy odwrotnie − zamiast twierdzenia drzewko, "bo tak to się robi". Niestety przy braku godzin lekcyjnych na matematykę, które usilnie przy kolejnych reformach "ucinano", nauczanie sprowadza się w wielu wypadkach do pokazywania "jak to się robi". tn, broń się sam przed zalewem bełkotu, nie zważając co będzie, a co nie będzie na egzaminach.

tn: Ok. To czy mozesz pokazać jakieś zadanie, rozwiązane w oparciu o całkowite?

PW: Wymyślmy coś. W magazynie znajdują się (w jednym pojemniku, nierozróżnialne) detale pochodzące z fabryk F₁, F₂, F₃. Z dokumentów wynika, że wielkości dostaw były odpowiednio w proporcjach 3:2:1. Wiadomo również, że fabryki te produkują odpowiednio 1%,3% i 2% wadliwych detali. Z pojemnika wyjęto losowo jeden detal. Oblicz prawdopodobieństwom że jest od dobry. Spróbuj sam, bez drzewka, powołując się na twierdzenie o prawdopodobieństwie całkowitym.

Mateusz: tn pisze przeciez a warto zebys sobie wszedł tez na strone cke chyba i przeczytał informator tam nie ma narzuconych metod rozwiązywania zadań to co jest to jest niezbedne minimum ktore kazdy maturzysta powinien znać a metod rozwiązania zadań jest tyle co samych zadań

tn: Ok. spróbuję zaraz. Aleś wymyślił

Mila: tn podaj linka do zadań maturalnych

tn: Przepraszam, że dopiero teraz. http://natablicy.pl/probna-matura-2013-z-oke-poznan-matematyka-poziom-podstawowy-i-rozszerzony-arkusz-test-zadania-przykladowe-odpowiedzi-rozwiazania,artykul.html?material_id=50e66cfcfbaedd9d18010000 @Mila, Sprawdzisz jedno rozwiązanie jak Ci pokażę ?

Mateusz: Zadanie dla tn proponuje ci zebys sobie zrobił dwiema metodami drzewkiem i policzył prawdopodobienstwo całkowite i porownaj sobie po pierwsze ile miejsca zajmie ci krzaczor a ile miejsca obliczenia. W skrzyni mamy pięć nowych i pięć używanych piłek. Przed grą tenisiści wybrali na chybił trafił ze skrzynki dwie piłki po grze wrzucili je z powrotem do skrzynki i znowu losowo wybrali dwie piłki. Oblicz prawdopodobieństwo, że za pierwszym razem wzięli dwie używane jeśli wiadomo że za drugim razem wylosowali dwie nowe.

tn: Ha, dzięki wielkie, ale jeszcze tamto muszę dokończyć Ale dzięki, że mas zmnie na uwadze, na pewno nie przeocze go

Mateusz: Spoko jak zrobisz to napisz odp zobacze czy sie zgadza jak nie bedzie sie zgadzała no to popracujemy i znajdziemy błąd .

tn: a te którymi pograli uznajemy za używane?

Mateusz: Tak jak najbardziej jesli w I etapie wylosowano nową piłke to po jej wykorzystaniu do gry musi ona byc traktowana w drugim etapie jako piłka uzywana.

tn: Są trzy przypadki: 1) Wzięli dwie używane 2) Wzięli dwie nowe 3) Wzięli jedną używaną, a jedną nową

Mateusz: Tak

tn: Musimy tutaj jakoś zastosować Prawdopodobieństwo warunkowe. Możesz zacząć za mnie to zadanie?

Mila: tn Pisz to rozwiązanie.

tn: Chodzi o zadanie 6. piszę takie założenia:

	π
(sinx > 0 ∧ sinx≠1 ∧cosx >0 ∧ cosx≠1 ) ⇒ x∊(kπ; kπ +		) ∧ k ∊ C
	2

	1
logsinxcosx +		= 2
	logsinxcosx

t = log_sinxcosx ∧ t>0

	1
t +		= 2
	t

t2−2t+1
	= 0
t

t=1 > 0 log_sinxcosx = 1 sinx = cosx

	π
czyli uwzględniając założenie x =		+ 2kπ ⋀ k ∊ C
	4

Mila: Napisz treść, bo nie mogę otworzyć pliku.

tn: Ok. Rozwiąż równanie log_sinxcosx + log_cosxsinx = 2

Mateusz: U− piłki uzywane N−piłki nieuzywane pierwszy etap doświadczenia mamy:

	5 2 5 0		2
P(UU1)=		=
	10 2		9

	5 1 5 1		5
P(UN1)=		=
	10 2		9

	5 0 5 2		2
P(NN1)=		=
	10 2		9

i teraz podobnie musisz rozpisac prawdopodobieństwa dla drugiego etapu wg tych przypadkow np w drugim etapie doswiadczenia gdy w pierwszym etapie wylosowano dwie nieuzywane piłki:

	5 2 5 0		2
P(UUII | UUI)=		=		i tak dalej liczysz dla tego warunku
	10 2		9

P(UN_II | UU_I) oraz P(NN_II | UU_I) dla reszty warunków analogicznie

Mila: Podstawowy mam, a jak znaleźć rozszerzony?

Mateusz: zrob a ja sprawze moze jeszcze dzis a jak nie to dopiero jutro Aha mam nadziej ze zapoznałes sie z prawdopodobienstwem warunkowym bo inaczej mozesz tych prawdopodobieństw nie rozumiec tzn dlaczego akurat takie są

tn: musisz tam wejść na drugą stronę

tn: https://matematykaszkolna.pl/strona/1023.html Ja nie rozumiem po prostu tej definicji. Jest taki wzór, ale mnie nic to nie mówi Wiem, że P(A) mogę rozpisać, ale co ma do tego jakieś P(B₁) etc

tn: Np. Warunkowe mniej więcej kapuję, ale to to jest jakieś dziwne. Mogę tak zapisać, ale co mi to daje ?

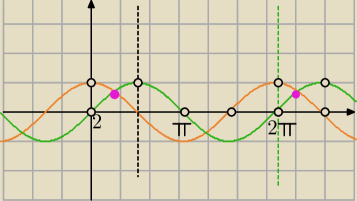
Mila: 1) sin x>0 i sinx≠1 i cosx>0 i cosx ≠1 [ krócej :sinx∊(0;1) i cosx∊(0;1)]

	π
⇔x∊(0+2kπ;		+2kπ)
	2

Więcej nie zauważyłam.

tn: Tak, oczywiście powinienem przecież dodawać pełny okres! Dzięki wielkie

Mateusz: Za skomplikowanej definicji troche uzywasz Mowiąc krócej jeśli zdarzenia losowe A₁,A₂,.......,A_n o dodatnich prawdopodobieństwach wykluczają sie nawzajem i suma ich jest zdarzeniem pewnym, to dla dowolnego zdarzenia losowego B jest prawdziwa zaleznosc: P(B)=P(A₁)*P(B|A₁)+P(A₂)*P(B|A₂)+...+P(A_n)*P(B|A_n) a jesli dalej tego nie widzisz to proponuje obejrzec sobie rysunek inaczej sie nie dało narysowac propornuje abys sobie to rozrysował na kartce ale tak jak pisał PW najwzniejsza jest tu sama definicja prawdopodobieństwa całkowitego a to jest tylko dla zobrazowania schematu.Drzewka owszem nadają sie do wieloetapowych −ale i bez nich wtedy tez sie mozna obejsc natomiast nie bardzo do doświadczeń dwu czy trzyetapowych−mozna ale po co z kolei P(D_s) / \ P(C_s) D_s C_s P(D_m |D_s) / \ P(C_m |D_s) P( D_m|C_s) / \ P(C_m | C_s) D_m C_m D_m C_m

tn: @Mateusz co oznacza zapis: P(UU₁) ?

tn: UP

tn: W magazynie znajdują się (w jednym pojemniku, nierozróżnialne) detale pochodzące z fabryk F1, F2, F3. Z dokumentów wynika, że wielkości dostaw były odpowiednio w proporcjach 3:2:1. Wiadomo również, że fabryki te produkują odpowiednio 1%,3% i 2% wadliwych detali. Z pojemnika wyjęto losowo jeden detal. Oblicz prawdopodobieństwom że jest od dobry. Zadanie od PW Załóżmy, że w pojemniku jest 6x detali. Tzn: I firma ma tam 3x detali II 2x detali III x detali. Wiadomo, że:

	11
0,01 * 3x + 0,03*2x + 0,02 * x =		x detali wadliwych w całym pojemniku
	4

	13x		11
Wiem, że Jest		udanych detali oraz		x wadliwych .
	4		4

Nie wiem, gdzie tu mógłbym rysowac drzewo bądź korzystać z p−stwa całkowitego. Jest jeden etap. Raz losuję i tyle. Na ile sposobów mogę wyciągnąc detal (wadliwy lub nie)

	13x
Na 6x (OMEGA) . Na ile mogę dobry?
	4

	13
Czyli P(A) =
	24

Mam poważne wątpliwości co do rozwiązania, toteż proszę o sprawdzenie

tn: (pozostaje mi jeszcze zadanie Mateusza)

PW:

	3		2		1
P(F1) =		, P(F2) =		, P(F3) =
	6		6		6

W − zdarzenie "wylosowano detal wadliwy". P(W|F₁) = 0,01, P(W|F₂) = 0,03, P(W|F₁) = 0,02 P(W) =P(W|F₁)^. P(F₁) +P(W|F₂)^. P(F₂)+P(W|F₃)^. P(F₃) Oczywiście policzyliśmy dopiero P(W), a prawdopodobieństwo wylosowania detalu dobrego to P(W') = 1−P(W). Tutaj można narysować to ulubione drzewko. najpierw z jednego punktu wychodzą trzy rozgałęzienia (fabryki), a potem z każdej fabryki − dwa rozgałęzienia (wadliwy lub dobry).

tn: No więc do dzieła: B₁ −Wzięli dwie nowe. B₂ − Wzięli jedną nową, druga starą. B₃ − Wzięli dwie stare. B₁ ∩ B₂ ∩ B₃ = ∅ B₁ ∩ B₂ ∩ B₃ = Ω Zatem zachodzi wzór na P−stwo całkowite: A − wylosowano dwie nowe. Jakie jest p−stwo, że na początku wzięli dwie używane? Nie mogę kontynuować tego zadania, jako, że go nie rozumiem. Co ma dla mnie do rzeczy czy potem wzięli takie czy takie. Byc może prawdopodobieństwo wylosowania dwóch nówek za drugim razem było skrajnie małe, ale akurat mieli takiego farta. Co zatem wprowadza fakt, że za drugim razem wylosowano nowe? Bez wątpienia będzie taka możliwośc.

tn: @PW, dlaczego moje rozumowanie jest błędne?

tn: Widzę PW, że osobno rozważasz najpierw jakiej firmy wylosujemy, a potem się martwisz, o p−stwo wadliwości. Ja jednak sobie zsumowałem i nie widze nic w tym złego.

PW: Nawet nie trzeba się wdawać w jakąś analizę, gdzie popełniłeś błąd. Wynik jest jawnie bzdurny −

	1
wyliczyłeś, że prawdopodobieństwo wylosowania dobrego detalu jest bliskie		(konkretnie
	2

	13
		), podczas gdy najgorsza fabryka produkuje 97% dobrych. Po zmieszaniu z lepszymi może
	24

być tylko lepiej.

Mateusz: Wiec idziemy dalej skonczylem na drugim etapie gdzie wylosowano dwie uzywane piłki wiec podobnie bierzemy sobie na tapete zdarzenie: w drugim etapie doswiadczenia gdy w pierwszym wylosowano jedną uzywaną i jedną nową piłke:

	6 2 4 0		5
P(UUII | UN1)=		=
	10 2		15

	6 1 4 1		8		8
P(UNII | UN1)=		=		=
	10 2		15		15

	6 0 4 2		2
P(NNII | NN1)=		=
	10 2		15

i teraz zostają nam ostatnie mozliwosci mianowicie w drugim etapie doswiadczenia gdy w pierwszym etapie wylosowano dwie nowe piłki:

	7 2 3 0		7
P(UUII | NN1)=		=
	10 2		15

	7 1 3 1		7
P(UNII | NN1)=		=
	10 2		15

	7 0 3 2		1
P(NNII | NN1)=		=
	10 2		15

No i nas teraz interesuje prawdopodobieństwo warunkowe:

	P(UU1∩NNII)
P(UU1 | NNII)=
	P(NNII)

Mateusz: Dwa razy kliknąłem niepotrzebnie idąc dalej otrzymujemy:

P(UU1)*P(NNII | UU1)
	=
P(NNII)

P(UU1)*P(NNII | UU1)
P(UU1)*P(NNII | UU1)+P(UN1)*P(NNII | UU1) + P(NN1)*P()

w mianowniku w ostatnim nawiasie gdzie jest * P() w nawiasie powinno widniec NN_II | NN₁ nie wpisałem tego bo mi wzor sypało bo był koniec linii. Tu tez mozesz do tego zadania narysowac drzewko nawet ci to proponuje mając wyliczone prawdopodobienstwa po rozwazeniu tych sytuacji i zobaczyc w ten sposob miejsce drzewek a defninicji

tn: @PW, @Mateusz dziękuję Wam bardzo za pomoc. Już sobie radzę z tymi zadaniami

Mateusz: No to sie bardzo ciesze z tego powodu a prawdopodbienstwo całkowite jak u ciebie?