zbiór wartosci
madziora: | | −1 | |
Zbiorem wartośći funkcji f(x)= |
| (x+4) 2+6 jest  jak to mam zrobic delta, nastepnie |
| | 3 | |
miejsce zerowe. współrzędne wierzchołka p i q i rysuje wykres, tylo problem mam z tymi
wsółrzędnymi. pomoże ktoś. plisss

28 gru 22:48
Eta:
z postaci kanonicznej
f(x)=a(x−x
w)
2+y
w
jeżeli a<0 parabola ramionami do dołu
to
ZW= (−∞, yw >
| | 1 | |
f(x)= − |
| (x+4)2+6 , a<0 i yw=6 |
| | 3 | |
to:
ZW= (−
∞, 6>
i to wszystko

28 gru 23:23
28 gru 23:23
pigor: ...., otóż z danej postaci masz wszystko co potrzebujesz :
a=−
13<0 , więc ramiona paraboli do dołu i q=y
w=4 , więc
Zw.={y: y≤4}=
(−∞;4> − szukany zbiór wartości funkcji f i to tyle . ...

28 gru 23:25
pigor: o kurcze , przepraszam − napisałem bzdurę ; oczywiście zamiast 4 powinno u mnie być 6

28 gru 23:27
Krzysiek : Funkcja −1/3(x +4)2+6 przeciez jest w postaci kanonicznej a ztej postaci to juz latwo odczytac
wspolrzedne wierzcholka p czyli xw a takze q czyli yw bo jest tak f(x)=a(x−p)2+q . Zbior
wartosci funkcji odzytujemy na osi OY wiec interesuje nasz wspolrzedna q czyli yw
wierzcholka u nas q czyli yw =6 a ramiona paraboli skierowane sa w dol bo a=−1/3 wiec jak
narysujesz sobie ta parabole to zauwazysz ze zbiorem wartosci funkcji (odczytujemy na osi OY)
bedzie przedzial (−∞,6>
Czyli jak masz postac kanoniczna fukcji kwadratowej to od razu odczytujesz wspolrzedne
wierzcholka .
Natomiast jesli masz postac ogolna lub iloczynowa to wtedy liczysz delte i wspolrzedna q
wierzcholka i wtedy odczytujesz zbior wartosci funkcji .
28 gru 23:32
Eta:
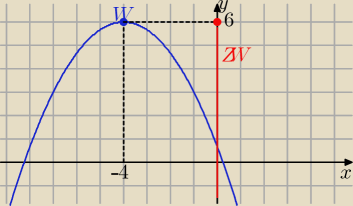
28 gru 23:37
29 gru 16:41
madziora: a ja głupia delte liczyłam podnosiłam do kwdratu masakra xD

dziękówki

29 gru 16:41
 jak to mam zrobic delta, nastepnie
jak to mam zrobic delta, nastepnie











 dziękówki
dziękówki 