pochodne
hej: kto pokaże jak to się robi?
zbadaj monotoniczność oraz istnienie ekstremów lokalnych funkcji f danej wzorem:
28 gru 16:28
Aga1.:
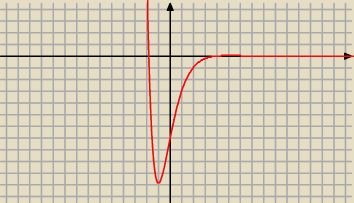
28 gru 16:58
Trivial:
Masz na przykładzie innej funkcji:
https://matematykaszkolna.pl/forum/99647.html
Na Twoim przykładzie:
| | x2−2x−7 | |
f(x) = |
| = (x2−2x−7)e−x |
| | ex | |
Funkcja f jest klasy C
1(R) → może mieć ekstrema tylko tam, gdzie zeruje się pochodna.
| df | |
| = (2x−2)e−x − (x2−2x−7)e−x = (−x2+4x+5)e−x |
| dx | |
Badamy monotoniczność.
| df | |
| > 0 ⇔ (−x2+4x+5)e−x > 0 ⇔ −x2+4x+5 > 0 ⇔ −(x+1)(x−5) > 0 ⇔ (x+1)(x−5) < 0 |
| dx | |
Funkcja rosnąca w (−1,5), malejąca w (−∞,−1) oraz (5,+∞).
Mamy ekstrema:
dla x = −1 minimum lokalne
dla x = 5 maksimum lokalne.
28 gru 17:00
hej: a skąd wiedziałaś jak to narysować?
28 gru 17:00
hej: | | 1+x | |
a jeżeli mam taką funkcje −−> f(x) = arctg |
| to jak to przekształcić jak nie mam ex |
| | 1−x | |
?
28 gru 17:06
Trivial:
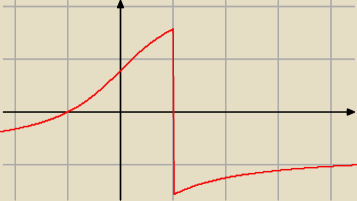
D
f: x≠1
Liczysz pochodną i już.
| df | | 1 | | (1−x) + (1+x) | | 2 | |
| = |
| * |
| = |
| |
| dx | | | | (1−x)2 | | (1−x)2+(1+x)2 | |
28 gru 17:23
hej: Trivial możesz mi jeszcze jedną zrobić?
f(x) = x2 −lnx2 ?
może teraz zrozumiem.
28 gru 17:51
28 gru 18:05
hej: Trivial nie moge sobie dać rady z tym arcusem co zacząłeś o 17:23, patrz:
w kolejnym kroku przyrównuje do zera to co wyszło:
x
2+2=0
x
2=−2
i wychodzi mi sprzeczne

więc jak dojść do ekstremów?
30 gru 15:26
hej: chyba żebym to rozpisał tak?
x2+2=0
(x+√2)(x+√2) = 0
to wtedy wyjdzie jedno zerowe
−√2?
30 gru 15:54

 Df: x≠1
Liczysz pochodną i już.
Df: x≠1
Liczysz pochodną i już.
 więc jak dojść do ekstremów?
więc jak dojść do ekstremów?