Oblicz pochodne michał: Oblicz pochodne a) f(x) = 3x² − 5x + 1

	1
b) f(x) = (√x + 1)(		− 1)
	√x

a) f'(x) = 6x − 5

	1		1		1		1
b) f'(x) =		−		−		−
	2x		2√x		2x2		2√x3

Dobrze?

ICSP: pierwsza dobrze. druga źle (najpierw wymnóż nawiasy a później licz pochodną )

michał: b) 0

	1 − x3
c) f(x) =
	1 + x3

	−6x2
f'(x) =
	x5 + 2x3 + 1

ICSP: b) nadal źle c) też źle − tutaj głupi błąd. Licznik jest dobrze policzony tylko w mianowniku powinno być zamiast x⁵ to x⁶. Najlepiej zostawiaj to w postaci : (1+x³)² − unikniesz takich błędów.

michał: d) f(x) = (1 + √x)(1 + x^1/3)(1 + x^1/4) f(x) = (1 + x^1/2)(1 + x^1/3)(1 + x^1/4) = 1 + x^1/3 + x^1/2 + x^5/6 + x^1/4 + x^7/12 + x^3/4 + x^26/24 dobrze to wymnożyłem?

	1		1		1
b) f(x) = (√x + 1)(		− 1) = 1 − √x +		− 1 = −√x +
	√x		√x		√x

	1		1
f'(x) = −		−
	2√x		2√x3

ICSP: teraz b jest moim zdaniem dobrze co do d wygląda

michał: ok to pochodna jest łatwa do obliczenia w d) więc kolejne przykłady: e) f(x) = (x² + 1)⁴

	x + 1
f) f(x) =
	x − 1

	x
g) f(x) =
	x2 + 1

e) f'(x) = 8x⁷ + 24x⁵ + 24x³ + 8x

	2
f) f'(x) = −
	x2 − 2x + 1

	1
g) f'(x) =
	x4 + 2x2 + 1

I jak obliczyć pochodną z czegoś takiego: h) f(x) = (1 + 2x)³⁰

michał: czy h) f'(x) = 30 * (2x + 1)²⁹ * 2 ?

ICSP: https://matematykaszkolna.pl/strona/359.html − ostatni wzór na pochodną funkcji złożonej − to do h oraz pierwszego e narazie zajmij się prostszymi: obydwa f oraz obydwa g + drugie e

Mila: Tak.

michał:

	1
i) f(x) = (		)1/3
	1 + x2

	1		1		1 + x2 + 2x
f'(x) =		* (		)−2/3 *
	3		1 + x2		1 + 2x2 + x4

świąteczny ICSP: i) pochodna funkcji zewnętrznej policzona dobrze. Pochodna wewnętrznej źle. Nie zapominaj o tym ze (1)' = 0 0 * (1+ x²) = 0

michał: fakt, więc:

	1		1		2x
i) f'(x) =		* (		)−2/3 *
	3		1 + x2		1 + 2x2 + x4

	1
j) f(x) =
	√1 − x4 − x8

	1
f'(x) =		* (−4x3 − 8x7)
	2 * √(1 − x4 − x8)3

świąteczny ICSP: michale podaj mi kolejność wzór z których skorzystałeś w przykładzie j.

michał: k) f(x) = 2^{x + 3} f'(x) = 2^{x + 3}ln2 * (x + 3)' = 2^{x + 3}ln2*1 l) f(x) = x10^x f'(x) = 1 * 10^x + x * 10^x * ln10

	x
m) f(x) =
	ex

	ex − xex
f'(x) =
	e2x

świąteczny ICSP: k l (ewentualnie wyciągnąć 10^x przed nawias m (ewentualnie wyciagnąć e^x przed nawias i skrócić z mianownikiem.

michał: w j) tam będzie

	1
f'(x) =		* (−4x3 − 8x7) teraz ok ?
	2 * √1 − x4 − x8

michał: n) f(x) = x²(x + 1)e^x = (x³ + x²)e^x = x³e^x + x²e^x f'(x) = 3x²e^x + e^xx³ + 2xe^x + e^xx² o) f(x) = e^xlogx

	1
f'(x) = exlogx + (logx)'ex = exlogx +		( ex}
	xln10

świąteczny ICSP: pierwsza wersja była dobra w j. Już troszkę późno jest i zaczynam się mylić

świąteczny ICSP: n i o chociaż w obydwu przypadkach możesz wyłączyć jeszcze e^X przed nawias

michał:

	logx
p) f(x) =
	ex

	ex   − exlogx xln10
f'(x) =
	e2x

q) f(x) = e^x2 f'(x) = e^x2 * 2x r) f(x) = x¹⁰logx

	x10
f'(x) = 10x9logx +
	xlog10

michał: s) f(x) = e^ex f'(x) = e^ex * e^x = e^{ex + x} t) f(x) = loglogx

	1		1
f'(x) =		*
	logxln10		xln10

u) f(x) = log₁₀(x − 1)

	1		1
f'(x) =		* (x − 1)' =		* 1
	(x − 1)ln10		(x − 1)ln10

świąteczny ICSP: wygląda dobrze. Jeszcze jutro rano postaram się to przejrzeć.

michał: v) f(x) = 10^{2x − 3} f'(x) = 10^{2x − 3}ln10 * (2x − 3)' = 10^{2x − 3}ln10 * 2 w) f(x) = 2^3x f'(x) = 2^3xln2 * (3^x)' = 2^3xln2 * 3^xln3

michał: a jak obliczyć coś takiego: x) f(x) = log₂|log₃(log₅x)|

michał:

Basiek:

	log5e		log3e		log2e
f'(x)=		*|		|*|		|
	x		log5x		log3(log5x)

Nie jestem pewna, co do modułów...

michał: Basiek Twoje raczej jest na pewno źle, ponieważ chyba jak jest moduł musimy rozpatrywać x > 0 i x < 0. Ale tego nie jestem pewny, więc pytam .

Basiek: Jeśli ugryziemy to tak, to.... dla log₃(log₅x)>0

	log5e		log3e		log2e
f'(x)=		*		*
	x		log5x		log3(log5x)

lub dla log₃(log₅x)<0 A tu już sprawa jest na tyle skomplikowana, że poprosiłabym o pomoc wujka Wolframa.

michał: może ktoś inny się wypowie?

Basiek: Przykro mi, że jestem niepomocna. Generalnie− nie zdałam tego kolosa. Masz może odpowiedzi, bo ciekawa jestem? I hm, skąd te przykłady?

michał: gdybym miał odpowiedzi nie zakładałbym tematu na forum, przykłady − z listy mam jeszcze wiele innych znacznie ciekawszych .

Basiek: Największa głupota świata to nie dać studentom odpowiedzi do zadań. Możesz sobie je robić w nieskończoność źle, sądząc, że jest okej. Powodzenia z pochodnymi, całkami i innymi.

michał:

michał: może ktoś pomóc?

michał: Mógłby ktoś pomóc z tym przykładem z wartości bezwzględnej ?

michał: pomocy

świąteczny ICSP: [C{Basia]] przecież Ci to zrobiła. Ufam jej na tyle aby nie sprawdzać jej rozwiązania.

michał: Ale które rozwiązanie jest prawidłowe? To co podałem, że trzeba rozpatrywać warunki?

świąteczny ICSP: chyba nie. | | jest podana tylko aby nie bawić się w jakieś trudniejsze ustalanie dziedziny.

michał: Znalazłem coś takiego: http://www.matematyka.pl/2329.htm

michał: Możesz odpowiedzieć? Czy to aby na pewno jest dobrze? Ponieważ w to wątpię.

świąteczny ICSP: jakoś nigdy za bardzo się nie bawiłem pochodnymi z wartością bezwzględną więc w tym temacie Ci za bardzo nie pomogę. Na pewno w jakiejś literatrzue będzie o tym napisane.

michał: będę musiał poczytać jeszcze o tym, a coś takiego: y) f(x) = e^√logx

	1
f'(x) = e√logx *
	xln10

z) f(x) = x^x2 f'(x) = x^x2 * 2x Czy w tym przykładzie z) będziemy musieli różniczkować? Jeżeli tak to dlaczego, jest jakiś uniwersalny schemat na to?

michał:

michał: :(

aniabb: poszukaj było na forum a na pewno jest w Krysickim

michał: Ale co było na forum? Jakbyś mogła dookreślić .

aniabb: przykład taki jak z)

michał: ale przecież ja obliczyłem pochodne i pytam tylko czy dobrze jest , a dobrze jest y) i z) ?

aniabb: https://matematykaszkolna.pl/strona/2223.html

michał: aha czyli z) jest źle a y)?

michał: z) f'(x) = (x^x2)' = e^lnxx2 = e^x2lnx = e^x2lnx * (x²lnx)' =

	1
= xx2 * (2x * lnx + x2 *		)
	x

Teraz będzie ok ?

aniabb: w y) brakuje mi pochodnej z pierwiastka

michał: y) f(x) = e^√logx

	1		1
f'(x) = e√logx *		*
	2√logx		xln10

teraz jest ok? I jakbyś mogła mi napisać jak zrobić przykład (post z godziny: 00:59 (24 grudnia) )

michał: a) f(x) = x^xx f'(x) = (x^xx)' = (e^lnxxx)' = (e^xxlnx)' = e^xxlnx * x^xlnx =

	1		1
= xxx * ( (1) * lnx + xx *		) = xxx * xx [ (lnx)2 + lnx +		]
	x		x

(1) (x^x)' = (e^lnxx)' = e^xlnx * xlnx = x^x * (lnx + 1) b) f(x) = x^√x f'(x) = (x^√x)' = (e^lnx√x)' = (e^√xlnx)' = e^√xlnx * (√xlnx)' =

	1		√x
= x√x * (		* lnx +		)
	2√x		x

c) a ja ruszyć takiego zwierza: f(x) = (logx)^x f'(x) = [(logx)^x]' = (e^ln(logx)x)' = (e^xln(logx)' = e^xln(logx) * (xln(logx))' =

	1		1
(logx)x * [ln(logx) + x *		*		]
	logx		xln10

dobrze zrobione są 3 powyższe przykłady ?

Mila: do 23:28 w (1) masz 3 piętrową choinkę, obliczyłeś pochodną z dwupiętrowej (dobrze), co jest potrzebne, aby dokonczyć zadanie (1), dalej dobrze.

	√x
b)dobrze, doprowadź do prostszej postaci ( usuń niewymierność z mianownika i wyłącz
	x

michał: czyli ogólnie dobrze? jakbyś mogła jeszcze napisać co z tą funkcją z wartością bezwględna o której wspominałem

Mila: c) dobrze, jutro jeszcze sprawdzę. Z wartością bezwzględną rozpisać

michał: d) f(x) = e^−x2logx

	1
f'(x) = (e−x2logx)' = −2xe−x2logx + e−x2*
	xln10

	1
e) f(x) = (√x −		)10
	√x

	1		1
f'(x) = 10 * (√x −		)9 * (√x −		)' =
	√x		√x

	1		1		1
= 10 * (√x −		)9 * (		−		) =
	√x		2√x		1   2√x

	1		1		2√x * 2√x
= 10 * (√x −		)9 * (		−		) =
	√x		2√x		2√x

	1		1 − 4x
= 10 * (√x −		)9 * (		)
	√x		2√x

f) f(x) = x⁵(x⁶ − 8)^1/3

	1
f'(x) = 5x4 * (x6 − 8)1/3 + x5 *		* (x6 − 8)−2/3 * 6x5
	3

Tego f) nie jestem zbyt pewny, czy potem też wyciągamy jeszcze funkcję złożoną. Jakby można prosić o ocenę tego c) z 23:28

michał: Milo ale jak rozpisać? mogłabyś zrobić przykładowo bo mam jeszcze kilka takich

Mila: Wyznacz najpierw wzór funkcji, który nie zawiera wartości bezwzględnej.

michał:

	1
g) f(x) = e2x + 3 * (x2 − x +		)
	2

	1		1
f'(x) = [e2x + 3*(x2 − x +		)]'=[e2x + 3*2(x2−x+		)] + e2x + 3 *(2x − 1)
	2		2

	1
h) f(x) = log
	1 + x

	1		1		1
f'(x) = (log		)' =		* (		)' =
	1 + x		1   ln10 1 + x		1 + x

	1		−1
=		*
	1   ln10 1 + x		(1 + x)2

	ex2
i) f(x) =
	ex + e−x

	ex2 * 2x * (ex + e−x) − ex2 * (ex − ex)
f'(x) =		=
	(ex + e−x)2

	ex2 * 2x * (ex + e−x)
=
	(ex + e−x)2

W tym wypadku możemy jeszcze coś poskracać, ale chcę wiedzieć czy to jest dobrze. A jeżeli chodzi i wypisanie wzoru czy chodzi o to: f(x) = log₂[log₃(log₅x)] przy założeniu, że log₃(log₅x) > 0

michał: a tamto d) e) i f) są dobrze?

Mila: f(x) = log₂|log₃(log₅x)| ; x>0 ( warunek dla najbardziej wewnętrznej funkcji) logarytmujemy tylko liczby dodatnie. a) f(x)=log₂(log₃(log₅x)) dla (log₃(log₅x))>0 (log₃(log₅x))>0⇔ log₃(log₅x)>log₃1⇔ log₅x>1⇔ log₅x>log₅5¹ 5x>5⇔x>1 Liczymy pochodną: (log₂(log₃(log₅x)))' b) |log₃(log₅x)|=−log₃(log₅x) dla (log₃(log₅x))<0 i x>0 rozwiąż warunek W punkcie zmiany wzoru policzyc pochone obustronne.

Mila: Dzisiaj już dobranoc, jutro wieczorem resztę.

michał: ok to wydaje się już proste zapewnę zaraz zrobię tylko dokończę tę listę co zacząłem.

michał: Dobranoc, dziękuję za pomoc . Jakby inni mogli sprawdzić też byłoby fajnie.

michał: Jakby ktoś mógłby sprawdzić przykłady zrobione przeze mnie o godzinie: 00:01 oraz 00:15 .

michał: może ktoś pomóc ?

Mila: W komentarzu 00:30 Pomyłka ( w edytorze źle widziałam za dużo piątek) 5 linijka od konca ma być: x>5 Pewnie to zauważyłeś przy ustalaniu dziedziny w drugim przypadku.

michał: A te inne przykłady są ok?

michał:

michał:

Mila: g) dobrze cd =e^2x+3*(2x²−2x+1+2x−1)= =2x²*e^2x+3 h) dobrze, doprowadź do prostszej postaci i) źle

michał: no dobrze, a przykłady d,e, f Bo ich raczej nie sprawdziłaś Milu

michał:

	ex2
i) f(x) =
	ex + e−x

	(ex2)' * (ex + e−x) − (ex + e−x)'*ex2
f'(x) =		=
	(ex + e−x)2

	ex2 * 2x * (ex + e−x) − (ex − e−x)*ex2
=
	(ex + e−x)2

Teraz jest ok

Mila: d, e f, też sprawdziłam, ale gdzieś zniknął komentarz.

	1		x−1
e)(√x−		)10=(		)10
	√x		√x

i teraz oblicz pochodną Wynik http://www.wolframalpha.com/input/?i=%28%28sqrt%28x%29-1%2Fsqrt%28x%29%29^%2810%29%29%27

Mila: f, i doprowadź do prostszej postaci.

michał: ale ogólnie dobrze? e czemu jest źle?

	x − 1		x + 1   2√x
10 * (		)9 * [		]
	√x		x

teraz ok? (przed skrócniem rzecz jasna)

Mila: Dobrze. Skorzystaj: (√x)⁹=(√x)⁸*√x

michał: ok zrobiłem to na kartce i wyszło j) f(x) = |x|³

⎧	x ≥ 0 f'(x) = 3x2
⎩	x < 0 f'(x) = −3x2

k) f(x) = sgnx Tego nie wiem jak ruszyć.

	⎧	0 dla x < 0
l) f(x) =	⎩	x2 dla x ≥ 0

	⎧	0 dla x < 0
f'(x) =	⎩	2x dla x ≥ 0

j) i l) dobrze? Jak zrobić to z sigmą?

Mila: i) można tak:

e2*ex		ex2+x
	=
ex*ex+e−x*ex		e2x+1

i teraz liczyć pochodną.

michał:

michał:

michał:

michał: może ktoś sprawdzić to z godziny: 00:03

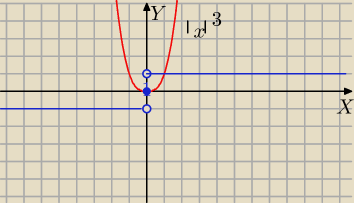
Mila: J) dobrze, zobacz wykres Y=|x|³ ( czerwony ) l) narysuj wykres f(x), jest dobrze. F(x)=sgn(x)=∫0 dla x=0 ∫ −1 dla x<0 ∫ 1 dla x>0 Brak pochodnej dla x=0 (funkcja nie jest ciągła w 0), dalej sam zrób.

michał:

michał: czyli:

	⎧	0 dla x = 0
f(x) = sgn(x) =	⎨	0 dla x < 0
	⎩	0 dla x > 0

michał: m) f(x) = e^−|x| f'(x) = { −e^−x dla x ≥ 0 &e^x dla x < 0} n) f(x) = √√1 + x² − 1

	1
f'(x) =		* (√1 + x2 − 1)' =
	√√1 + x2 − 1

1		1
	*		* 2x
√√1 + x2 − 1		2√1 + x2

o) f(x) = {x} Tego nie wiem jak ruszyć.

	⎧	x dla x < 0
p) f(x) =	⎩	x2 dla x ≥ 0

	⎧	1 dla x < 0
f'(x) =	⎩	2x dla x ≥ 0

q) f(x) = sgn(x⁵ − x³) i tutaj nie wiem jak narysować ten wykres do tego

michał: czy w tym q) x²(x³ − 1) = 0 ⇔ x²(x − 1)(x² + x + 1) czyli pochodna będzie x ∊ R \ {0, 1}

michał:

Mila: 16:00 brak pochodnej w zerze, napisałam! Czytaj, co piszę. f '(x)=0 dla x<0 f '(x)=0 dla x>0 m) w punkcie zmiany wzoru liczysz pochodne obustronne z definicji.

Mila: q) f(x) = sgn(x⁵ − x³) x⁵−x³=0 x³(x²−1)=0 x=0 lub x=1 lub x=−1 x⁵−x³>0 x³(x−1)(x+1)>0⇔x∊(−1;0)∪(1;∞) f(x)=sgn(x⁵−x³)=1 dla x∊(−1;0)∪(1;∞) w tej dziedzinie f'(x)=0 f(x)=sgn(x⁵−x³)=−1 dla x∊(−∞;−1)∪(0;1) w tej dziedzinie f'(x)=0 sgn(x⁵−x³)=0 dla x∊{−1,0;1} punkty nieciągłości tu brak pochodnej

Mila: o) f(x) = {x} część ułamkowa liczby (mantysa), jest wiki, zobacz jak wygląda .

michał: a p) i n) dobrze? czyli m) będzie: f'(x) = e{−|x|} * −|x| i teraz z tymi warunkiami?

	⎧	e−x * −1 dla x ≥ 0
f'(x) =	⎩	ex * 1 dla x < 0

czy coś mylę ?

michał:

Mila: m) f(x)=e^−x dla x≥0 pochodna: f '(x)=−e^−x dla x>0

	e−(0+h)−e0
limh→0+		=−1
	h

f(x)=e^x dla x<0 pochodna f ' (x) =e^x

	e(0+h)−e0
limh→0−		=1⇒pochodna w zerze nie istnieje.
	h

Mila: p) zbadaj w zerze.

michał: a to zawsze musimy badać coś takiego w zerze? Czy o co z tym chodzi, że tak zapisałaś Milo ?

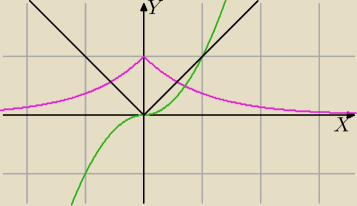
Mila: Jeśli funkcja jest podana dwoma wzorami to tak. 1) Na wykresie f(x)=e^−|x| w zerze mamy "szpic" 2) Np. funkcja f(x)=x|x| ma pochodną w zerze (zielony wykres) zbadaj z definicji pochodną 3) a funkcja g(x)=|x| nie ma pochodnej w zerze.(czarny, też w zerze jest "szpic") Jeśli na kolokwium nie będziesz tego umiał, to napisz, przykładowo g(x)=x dla x≥0 i g '(x)=1 dla x>0 g(x)=−x dla x<0 i g ' (x) =−1 dla x<0 Będzie zadanie niedokończone. Uwaga − nie ma pochodnej w "urwiskach" i szpicach. Na pewno miałeś to omówione na wykładach albo ćwiczeniach.

michał: aha ok teraz to rozumiem Tylko jak dokończyć to z częścią ułamkową. Wiem, że {x} = [x] − x, ale jak z tego wyliczyć pochodną?

	π10
r) f(x) =		czy pochodna z tego będzie wynosiła 0? Bo teoretycznie mamy same
	π − e

liczby .

michał:

Mila: 1) r) 0 2) f(x)={x}⇔ f(x)=x−[x} wydaje mi się po wykresie sądząc: w x=k, gdzie k∊C brak pochodnej dla x∊R\{k}; k∊C f '(x)=1 ale, nie mam pewności. Poszukam w literaturze, to potwierdzę lub zaprzeczę.

michał: czyli: v) f(x) = e^e f'(x) = 0 u) f(x) = (x + e)²⁰ f'(x) = 20 * (x + e)¹⁹ * 1 t) f(x) = x⁷ + e² f'(x) = 7x⁶

	⎧	ex dla x < 0
s) f(x) =	⎩	1 + x dla x ≥ 0

f'(x) = U{e^x dla x < 0 &1 dla x ≥ 0} i tutaj chyba powieniem zbadać jeszcze te krańce o których pisałaś , zgadza się?

Mila: s) Tak, ale tam istnieje pochodna w x=0

michał: a reszta jest ok?

Mila: Tak.

michał: ok, to z tych przykładów koniec teraz zostały mi jeszcze takie: f(x) = ³√x². Oblicz f'(8) korzystając z definicji. Definicje znam:

	f(xo + h) − f(xo)
f'(xo) = limh → 0
	h

Tylko potem gubie się przy przekształceniach: f(8) = ³√64 = ³√4 * 4 * 4 = 4 f(8 + h) = ³√(8 + h)² = ³√64 + 16h + h²

	3√64 + 16h + h2 − 4
f'(8) = limh→0
	h

i nie wiem co poczynić dalej

michał:

Mila: korzystam z wzoru:a³−b³=(a−b)(a²+ab+b²) a=³√(8+h)² b=³√64=4

3√(8+h)2−4		(3√(8+h)2)2+43√(8+h)2+42
	*		=
h		(3√(8+h)2)2+43√(8+h)2+42

	(8+h)2−64
=		=
	(8+h)3√h*((8+h)+43√(8+h)2+16)

	64+16h+h2−64
=		=
	h*((8+h)3√((8+h)+43√(8+h)2+16)

16+h		16		1
	→		=
((8+h)3√((8+h)+43√(8+h)2+16		8*2+4*4+16		3

michał: nie ma błędu w 5 i 6 linijce? w mianowniku?

michał: jest błąd z nawiasikami, poza tym wszystko wydaje się ok A wiesz może jak wyprowadzić wzór f'(x) [z def.] gdy f(x) = x⁵

Mila: Tam w jednym miejscu h nie powinno być pod pierwiastkiem, łatwo zrobić błąd przy takim edytorze. Napisz ostatni przykład, to sprawdzę.Skorzystaj z dwumianu Newtona.

michał: f(x) = x⁵ f'(x) = 5x⁴

	(xo + h)4 * (xo + h) − xo
f'(x) = limh→0		=
	h

	xo5 + 5xo4h + 10xo3h2 + 10xo2h3 + 5xoh4 + h − xo
=		co dalej?
	h

	5 0		5 1		5 2		5 3
(xo + h)5 =		xo5 +		xo4h +		xo3h2 +		xo2h3 +

5 4		5 5
	xoh4 +		h

(x_o + h)⁵ = x_o⁵ + 5x_o⁴h + 10x_o³h² + 10x_o²h³ + 5x_oh⁴ + h

Mila: f(x)=x⁵

	f(x+h)−f(x)
Limh→0		=
	h

	(x+h)5−x5
=limh→0		=
	h

	x5+5x4*h+10x3*h2+10x2*h3+5xh4+h5−x5
=limh→0		=
	h

	5x4*h+10x3*h2+10x2*h3+5xh4+h5
=limh→0		= skracam przez h
	h

f '(x)=lim_h→0(5x⁴+10x³*h+10x²*h²+5xh³+h⁴)=5x⁴

Mila: DOBRANOC.

michał: faktycznie chciałem skracać ale nie pasowało mi bo pomyliłem się w zapisie na końcu i napisałem x^o Zostało mi ostatnie zadanie z tej listy:

	⎧	|x| : |x| ≥ 1/n
fn(x) =	⎩	ax2 + bx + c : |x| < 1/n

Mamy określić a,b,c, aby f_n(x) była różniczkowalna. Ponadto mamy obliczyć f'_n(x). Co znaczy dokładnie, że funkcja jest różniczkowalna? I jak to w ogóle ruszyć?

michał: ok, dziękuję bardzo za dzisiejszą pomoc. dobranoc

michał:

michał:

michał: Mila możesz pomóc ?

Mila: Powiedz mi, z jakich studiów to zadanie? Zaraz później coś tam napiszę. Jakoś nikt nie chce się do nas dołączyć.

michał: pierwotnie studiuję ekonomię, a takie zadanie dostałem na liście

michał:

Mila: Wyznaczyłam wzór , ale...? mam wątpliwości.

	1		1
|x|≥		dla x≥1 lub x≤−1 {|−1|=1; |1|=1;		=1 równość dla x=−1 i x=1 i wykres leży
	n		1

powyżej pomarańczowych punktów) f_n(x)=x dla x≥1 lub f(x)=−x dla x≤−1 teraz w środku spróbuj wyznaczyć f'(x)=2ax+b i pochodna w punkcie x=1 lub x=−1 ma być równa wartości pochodnych wyznaczonych funkcji. Czy bardzo Ci się śpieszy?

michał: chciałbym to juz skończyć , ale mogę poczekać (chodź mam jeszcze 9 innych zadań)

Mila: Wyznacz ten wzór, młoda głowa niech pomyśli.Zobaczymy, czy zeznania będą zgodne.

michał: wiedziałbym jak to ruszyć gdyby nie było tego "n" o co dokładnie z tym chodzi ?

Mila:

1
	to ciąg, jego wykres ( początek) masz u góry
n

Chodzi o to, że |x| leży powyżej punktów pomarańczowych albo poniżej. Jeśli nie masz pomysłu, to rób następne zadania.

michał: ok to mam takie: a) f(x) = x² + 2x + 21 [−2, 7] b) f(x) = |x + 1| + x², [−10, 10] I polecenie: znaleźć min i max wartość w/w f(x) w danych przedziałach. I a) zrobiłbym normalnie jak w liceum, x_w, potem podstawiamy tylko tutaj pewnie muszę coś z pochodnymi i nie mam pomysłu jak.

michał: jakiś pomysł? może jest na to jakiś schemat?

michał: chodzi o to: a) f(x) = x² + 2x + 21 [−2,7] Funkcja tutaj może zmienić znak tylko w wierzchołku zatem badamy jego pochodną: f'(x) = 2x + 2, zatem wierzchołek ma punkt x = −1 Zatem musimy rozpatrzyć 3 punkty: f(−1) = 20 f(−2) = 21 f(7) = 84 Zatem min f(−1), max f(7) zgadza się? b) jak zacząć tutaj? i jak to rozpatrywać, myślę, że trzeba będzie coś z przedziałami. Można prosić o dokładny opis takiego przypadku ?

michał: b) f(x) = |x + 1| + x² [−10, 10] Będziemy rozwżali punkty −1, −10, 10. Sprawdźmy gdzie zeruje się pochodna. Rozważmy wpierw

	1
przedział: (−10, −1). W tym przedziale f(x) = −x − 1 + x2, więc f'(x) = 2x − 1 ⇒ x =		.
	2

A to nie należy do przedziału więc nasza funkcja się nie zeruje. Rozważmy drugi przedział:

	1
(−1, 10). Mamy wówczas f(x) = x + 1 + x2, czyli f'(x) = 2x + 1 ⇒ x = −		. Znaleźliśmy
	2

punkt w którym pochodna się zeruje. Więc rozważamy wartości: f(−10) = 109 f(10) = 111 f(−1) = 1

	1		1		1		1		2		3
f(−		) =		+		=		+		=
	2		2		4		4		4		4

	1
Min f(−		), Max f(10)
	2

Może tak być?

michał: To może zrobie jeszcze c) f(x) = |x² − 1| + 3x [−2,2] Tak jak wyżej będę rozpatrywał punkty −2, 1, −1, 2. Wpierw rozpatrzę przedziały: (−2, −1), (−1, 1), (1, 2). Te 3 przedziały będą ok? I dla którego teraz tutaj opuszczę wartość bezwględną tj.: gdzie nie postawię minusa?

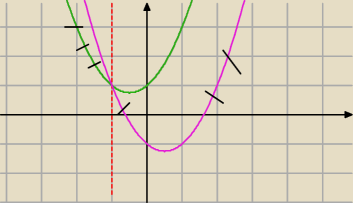
Mila: a) dobrze ( nie sprawdzałam wartości tylko metodę) pomagaj sobie rysunkiem, jesli prosta funkcja w odpowiedzi napisz wartości min i max b) przedziałami. x+1≥)⇔x≥−1 f(x)=x²+x+1 (zielona z prawej) dla x≥−1 f(x)=x²−x−1 różowa z lewej strony prostej x=−1 minimum ma funkcja zielona a maksimum liczysz f(10) =10²+10+1 f(−10)=10²−(−10)−1 i wybierasz

michał: A można to zrobić tak jak ja zrobiłem? i czy c) rownież będzie ok tylko gdzie tam minus usunąć ?

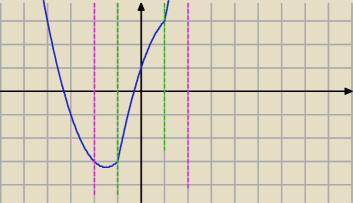
Mila: w b) trochę przekombinowałeś i to może się nie podobać, nie będzie mu się chciało sprawdzać? c)Tak, 3 przedziały x²−1≥0⇔x≤−1 lub x≥1 |x²−1|=x²−1 dla x≤−1 lub x≥1⇔ f(x)=x²−1+3x dla x≤−1 lub x≥1⇔

	3
xw=−		i badaj
	2

f(x)=−x²+1+3x dla x∊(−1;1)

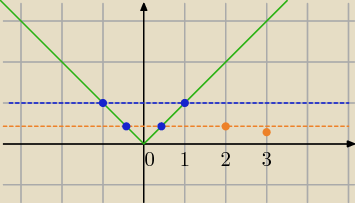
Mila: ostatnie zadanie z tej listy: ⎧ |x| : |x| ≥ 1/n f_n(x) =⎩ ax² + bx + c : |x| < 1/n Mamy określić a,b,c, aby f_n(x) była różniczkowalna. Ponadto mamy obliczyć f'_n(x). n∊N₊

	1
fn(x)={x dla x≥		wtedy f '(x)=1
	n

	1
{−x dla x<−		wtedy f '(x)=−1
	n

	1		1
{ ax2+bx+c dla x∊(−		;		)
	n		n

Badamy różniczkowalność w punktach zmiany wzoru.

	1		1		1		1
(		;		) i (−		;		)
	n		n		n		n

	1
[ na wykresie widać:an=
	n

dla n=1 a₁=1 |1|=1 i |−1|=1

	1		1		1		1		1
dla n=2 ; a2=		; |		|=		i|−		|=		] Przeanalizuj!
	2		2		2		2		2

	1		1
f 'n(x)=2ax+b dla x∊(−		;		)
	n		n

aby f_n była różniczkowalna w całej dziedzinie to muszą pochodne "sklejanych" funkcji być równe w punktach zmiany wzoru

	1		1		1		−1
f 'n(		)=1 i f ' n(−		)=−1⇔2a*		+b=1 i 2a*		+b=−1
	n		n		n		n

	n
stąd b=0 i a=
	2

	n
fn(x)=		x2+c w punktach zmiany wzoru musi zachodzić równość
	2

wartości sklejanych funkcji

	1		n		1		1		1
fn(		)=		*		+c=		stąd c=
	n		2		n2		n		2n

reasumując:

	1
fn(x)={x dla x≥		wtedy f '(x)=1
	n

	1
{−x dla x<−		wtedy f '(x)=−1
	n

	n		1		1		1
{		x2+		dla x∊(−		;		) f'n(x)=... oblicz
	2		2n		n		n

Posprawdzaj rachunki, bo mogłam źle przepisać.

michał: ok (chyba) to rozumiem dziękuję bardzo za szczegółowe wyjaśnienie, tymczasem odnośnie min i max mam jeszcze 3 przykłady których nie do końca rozumiem, wówczas:

	x
a) f(x) = log(x) −		[1, e3]
	10

b) f(x) = x^1/x [2,4] c) f(x) = 3sin(x) + sin(3x) [0, 2π] Jakbyś mogła napisać jak to zacząć czy w a) wystarczy obliczyć tylko pochodną? i podstawić wówczas punkty: 1, e³

	1
f'(x) =		− {1}{10}
	xlog2

1		1
	=		/ * log2
xlog2		10

1		log2
	=
x		10

	10
x =
	log2

(w zadaniu podano, że jeżeli logx to podstawa wynosi 2)

Mila: Badasz jak zachowuje się pochodna (gdzie dodatnia, ujemna , zero, i jak to wygląda w podanym przedziale.

	1
a) f '(x) =		−0,1
	xln(2)

Załóż nowy post, bo trzeba "przewijać" stronę.

michał: no tak jak pisałem? tylko zamiast log ln ?

	10
czyli: x =		i nie wiem czy to należy do przedziału
	ln2

bo chyba ln_e2 zgadza się? ( a temat zaraz założę), a to chyba należy bo będzie > 1 i < e³ tak mi się wydaje .

Artur_z_miasta_Neptuna: ln2 <1 ... bo 2<e ⋀e>1 więc x <0

Artur_z_miasta_Neptuna: tfu tfu ... ln2<0 oczywiscie mialo być

michał: to ln2 nie należy do [1, e³] Więc tylko rozpatrywać 1 i e³ czy jak ?

Mila: Badamy znak pochodnej w przedziale <1;e³≈20,1> ln2≈0,7

10
	≈14,3∊<1;e3>
ln2

1		1
	−		>0 i x≥1
xln2		10

1		1
	>		/*10
xln2		10

10
	>1 /( mogę pomnożyć przez xln2 >0 )
xln2

10>xln2

	10
x<		≈14,3 pochodna dodatnia ,
	ln2

	10
dla 1<x<		funkcja f(x) rosnąca
	ln2

	10
dla x=		maksimum
	ln2

	10		ln10−ln2		1
f(		)=		−
	ln2		ln2		ln2

wartość najmniejszą licz na końcach przedziału ( będzie w 1.)

michał: jakbyś mogła Milo napisać skąd wzięła Ci się ta nierówność? na jakiej podstawie? i jak np.: ruszyć b)

michał: mógłby ktoś napisać skąd wzięła się ta nierówność ?

michał:

Mila: Konkretnie, to o którą nierówność pytasz? b) zbadaj znak pochodnej w podanym przedziale, ewentualne ekstremum.

michał: pytam o te ">" oraz "<" na jakiej podstawie, ponieważ lubię wszystko teoretycznie .

Mila:

	1		1
Napisałam nierówność:		−		>0
	xln2		10

ponieważ chcę wiedzieć w jakim przedziale ( przedziałach) f(x) jest rosnąca, czy pochodna zmienia znak przy przejściu przez miejsce zerowe, bo wtedy f(x) ma ekstremum.

michał: problem jest taki, że nie miałem jeszcze extremum

Mila: Badania przebiegu funkcji nie miałeś?

michał: <niee>

Mila: W takim razie, zadania wybiegają poza tematykę przerobioną. 1) Albo zostawisz te zadania, zbadasz tylko podstawowe funkcje, liniową, kwadratową, homograficzna i nie liczysz wtedy pochodnych, bo nie wiesz co z nimi zrobić, 2) Albo sam uczysz się teorii i badasz przebieg funkcji.

michał: a jak zbadać znak pochodnej w b), o co dokładnie chodzi z tą wskazówką ?

Mila: Jeśli pochodna dodatnia to funkcja jest rosnąca, jeśli ujemna to funkcja jest malejąca. Rozwiązujesz nierówność: f'(x)>0

Mila: w zadaniu b) licz na końcach przedziału. f(2)=2^1/2=√2 f(4)=⁴√4=⁴√2²}=√2 Zapomniałam, o tym, że jeszcze możesz korzystać z własności funkcji wykładniczej i logarytmicznej.

M: Proszę o pomoc z policzeniem pochodnych tych funkcji : f(x) = e^x (x⁴ + 16) f(x)=e²x / x⁵

Janek191: f(x) = e^x *( x⁴ + 16) f ' (x) = ( e^x)' *( x⁴ + 16) + e^x *( x⁴ + 16 ) ' = e^x*( x⁴ + 16) + e^x*( 4 x³) = = e^x*( x⁴ + 4 x³ + 16)

Janek191: Przepisz II funkcję, bo nie wiadomo co tam jest ?

	e2x
Czy f(x) =		?
	x5

paula: Oblicz wspolrzedne punktow przecięcia sie wykresu funkcji f z osiami ukladu wspolrzednych . Narysuj wykres każdej funkcji. A) f(x)=4x pomocyyyy

paula: B) f(x) = − x