zadania typu "wykaż" krecik: Zadania typu "wykaż" −−−−− tylko dla maturzystów zad.1/ Wykaż,że pole trapezu równoramiennego, którego przekątna ma długość"m" i tworzy z dolną podstawą kąt α

	m2*sin2α
jest równe: P=
	2

zad.2/Wykaż,że jeżeli miary kolejnych kątów czworokąta wypukłego tworzą ciąg arytmetyczny o różnicy 50^o, to ten czworokąt jest trapezem . zad.3/Wykaż,że jeżeli trapez jest równoramienny o podstawach a>b i jest opisany na okręgu, to długość jego wysokości jest równa średniej geometrycznej długości jego podstaw. zad.4/ Wykaż,że w dowolnym trapezie o podstawach a>b, odcinek łączący

	a−b
środki przekątnych trapezu ma długość :
	2

zad.5/Wykaż, że w trójkącie prostokątnym, wysokość i środkowa poprowadzone z wierzchołka kąta prostego tworzą z przyprostokątnymi kąty o równych miarach. zad.6/ Bok prostokąta ma długość 24 , a jego przekątna ma długość 26. W każdy z trójkątów, na które podzieliła ten prostokąt przekątna wpisano okręgi. wykaż,że odległość między środkami tych okręgów jest równa 4√17 a matura ... tuż, tuż za 137 dni

Patryk: w a) a+b=m ?

Saizou : a mogę też rozwiązywać? Bo ja nie jestem maturzystą tylko w 2 LO

krecik: Seria liczby : typu "wykaż" 1) Wykaż,że jeżeli n€N i n nie jest podzielna przez 3, to liczba n²+2 jest podzielna przez 3 2) Wykaż,że liczba 2²⁰⁰⁰ −16 jest podzielna przez 240 3) Wykaż, że jeżli liczby x i y są całkowitymi i x jest wielokrotnością liczby 3 i x≠3y to liczba

	x2−9y2
		−−− jest liczb całkowitą
	3x−9y

4) Wykaż,że dla każdej liczby całkowitej "k" liczba: (k+2)⁴−k⁴ jest wielokrotnością liczby 8 5) Wykaż,że dla a >0 zachodzi:

	8		4
		−		+a ≥2
	a2		a

6) Wykaż,że dl dodatnich liczb a, b, c zachodzi nierówność

	a		b		c
		+		+		≥3
	b		c		a

7) Wykaż,że reszta z dzielenia sumy kwadratów czterech kolejnych liczb parzystych jest równa 8

krecik: Możesz...... Saizou

tech: zad 1: n²+2=n²−1+3=(n−1)(n+1)+3 są to dwie liczby naturalne, wśród których jedna jest podzielna przez 3 Może tak być?

Saizou : wieżźy dwie liczby naturalne 1 i 2 czy one są podzielne przez 3

Saizou : *weźmy

Saizou : a zadanie 7 chyba jest wybrakowane

tech: jak podstawimy za n=1 wyjdzie z pierwszego nawiasu 0, a więc całość = 3 jak podstawię za n=2 to z drugiego nawiasu wyjdzie 3, a to jest podzielne przez 3 żle myślę?

Saizou : myślisz dobrze ja tam widziałem napisane 2 kolejne liczby naturalne

tech: dla mnie właśnie najgorsze są te zadania, a na maturce zawsze są

Saizou : to trzeba ćwiczyć praktyka czyni mistrza

Maslanek: Z tym n²+2, łatwiej chyba: n=3k n=3k+1 n=3k+2.

Saizou : możesz napisać że jest to iloczyn liczby parzystej i nieparzystej zatem na pewno dzieli się przez 3

Maslanek: Raczej dwóch parzystych lub dwóch nieparzystych ^^

krecik: Fakt zad7/ ma być...... z dzielenia przez 16

tech: zad.4 (k+2)⁴−k⁴=((k+2)²−k²)((k+2)*2+k²)=(k²+4k+4−k²)(k²+4k+4+k²)=(4k+4)(2 k²+4k+4)=4(k+1)2(k²+2k+2)=8(k+1)(k²+2k+2)

krecik:

tech: zad. 5: 8−4a+a³−2a²≥0 a³−2a²−4a+8≥0 a²(a−2)−4(a−2)≥0 (a²−4)(a−2)≥0 (a−2)(a+2)(a−2)≥0 (a−2)²(a+2)≥0 a ta nierówność jest zawsze prawdziwa

krecik: ok wysłałbym Ci ponownie ale Eta zabrała mi wszystkie jabłuszka

Saizou : właśnie sobie to uświadomiłem , że parzystych albo nieparzystych

Saizou : zad 7 W(x)=(2x)²+(2x+2)²+(2x+4)²+(2x+6)²= =4x²+4x²+8x+4+4x²+16x+16+4x²+24x+36= =16x²+48x+56=16(x²+3x+3)+8 cnu

Saizou : zad. 3 niech x=3t t∊C

9t2−9y2		t2−y2		(t−y)(t+y)
	=		=		=t+y
9t−9y		t−y		t−y

cnu

tech: a wiesz moze jak 2 zrobić? Bo myślę, myślę i nic

tech: 2²⁰⁰⁰−16=2²⁰⁰⁰−2⁴=2²⁰⁰⁰−2⁸+240 tylko co dalej?

krecik: zad.7/ i 3/ zaliczone

krecik: https://matematykaszkolna.pl/forum/79846.html

Maslanek: 2²⁰⁰⁰−16=2⁴(2¹⁹⁹⁶−1). Rozkładać 2¹⁹⁹⁶−1? Trochę szaleństwo, ale zawsze to jakaś metoda

Kejt: no właśnie też nad tym myślałam..trzeba rozłożyć to do postaci: 2⁴(2⁴−1)(.....) chyba, ze da się jakość szybciej..

Maslanek: Albo jeszcze trochę inaczej: 16(4⁹⁹⁸−1). Więc 4⁹⁹⁸−1=16⁴⁹⁹−1 musi być podzielne przez 15. Jak wiadomo liczba x^y jest podzielna przez x. Więc skoro 16⁴⁹⁹ jest podzielna przez 16, to 16⁴⁹⁹−1 jest podzielna przez 15. Zatem mamy taką podzielność

Saizou : albo ze wzoru 16⁴⁹⁹−1=(16−1)(16⁴⁹⁸+16⁴⁹⁷+...+16+1)

krecik: Saizou

krecik: Saizou

krecik: Dwa razy się "wkopało"

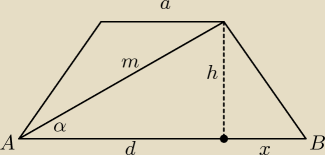
Saizou : zad. 1 z geometrii x=d−a lABl=d+x=d+d−a=2d−a

	h
sinα=
	m

h=msinα

	d
cosα=
	m

d=mcosα lABl=2mcosα−a

	(a+2mcosα−a)msinα		m2*2sinαcosα		m2sin2α
P=		=		=
	2		2		2

cnu

krecik:

Saizou : zad. 4 geometria ładny jest dowód na wektorach (piszę bez zapisu strzałek nad wektorami)

	1		1
EF=		CA+AB+		BD
	2		2

	1		1
EF=		AC+CB+		BD (dodając stronami)
	2		2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 2EF=AB+CB+BD CB=CD+DB 2EF=AB+CD+DE+BD 2EF=AB+CD

	AB+CD
EF=
	2

	a−b
EF=		bo wektor CD jest przeciwny do b
	2

zatem (kończąc zapis wektorowy)

	a−b
EF=
	2

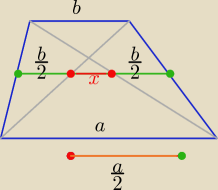
krecik: Z podobieństwa odpowiednich trójkątów ( nie chce mi się już pisać

	a		b		a−b
i x=		−		=
	2		2		2

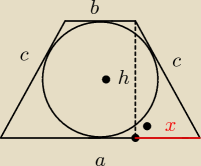
Saizou : zad 3 z geometrii a+b=2c

	a+b
c=
	2

	a−b
x=
	2

z tw. pitagorasa

	a−b		a+b
(		)2+h2=(		)2
	2		2

a2−2ab+b2		a2+2ab+b2
	+h2=
4		4

a²−2ab+b²+4h²=a²+2ab²+b² 4h²=4ab h²=ab h=√ab cnu

Kejt: ostało się coś jeszcze? jakieś reszteczki...

Saizou : z geometrii 2,5,6 a z liczb rzeczywistych 6 jeśli wszystko dobrze policzyłem

Saizou :

	2P		240
r=		=		=4
	a+b+c		60

lBCl=24−2r=24−8=16 lACl=10−2r=10−8=2 lABl²=2²+16² lABl²=260 lABl=2√65 tylko co tu nie pasuje

Kejt: ok, to ja powalczę z 6.

Eta: Hej Saizou odp: |AB|= 2√65 −−− jest poprawna ( wpisałam błędną odp ... sorry

Kejt: obrażam się na to 6

Maslanek: Co do 6: Mamy x−długość odcinka od wierzchołka do punktu styczności (jednocześnie promień okręgu wpisanego) Więc: p²=(24−2x)²+(10−2x)²

	a+b−c
Gdzie x (promien okręgu wpisanego w trójkąt prostokątny): x=		={24+10−26}{2}=4.
	2

Wtedy p²=16²+2²=260 Ee... Brakuje 12j²... Dziwne

Kejt: 2. niestety nie mogę zrobić rysunku, bo mi się coś zacina a₁;a₂;a₃;a₄ −> kąty wewnętrzne, oznaczano kolejno w kierunku przeciwnym do wskazówek zegara, zaczynając od kąta na dole po lewej stronie. r=50^o a₂=a₁+50^o a₃=a₁+100^o a₄=a₁+150^o skoro czworokąt to: a₁+a₂+a₃+a₄=360^o a₁+a₁+50^o+a₁+100^o+a₁+150^o=360^o 4a₁+300^o=360^o 4a₁=60^o a₁=15^o a₂=65^o a₃=115^o a₄=165^o aby był trapezem musi zajść związek: a₁+a₄=180^o i a₂+a₃=180^o a₁+a₄=15^o+165^o=180^o a₂+a₃=65^o+115^o=180^o czworokąt ten jest trapezem. c.n.u i moje pytanie..jeśli zachodzi taka zależność między kątami...to on na pewno jest trapezem?

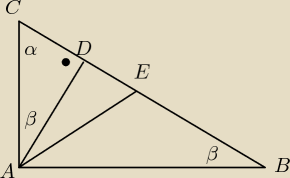
Saizou : trójkąty ABC i ACD są podobne zatem kąt CAD= ABC=β lAEl=lBEl ponieważ są to promienie okręgu opisanego na trójkącie ABC zatem kąt BAE=ABE=β, wówczas kąt CAD=BAE cnu

Godzio: Kejt, niekoniecznie ! Jeżeli jest to trapez to jasne jest, że spełniona jest taka zależność, ale w drugą stronę już nie za bardzo. Co to jest trapez ? To jest czworokąt, który posiada jedną co najmniej jedną parę boków równoległych − na tym powinnaś się opierać

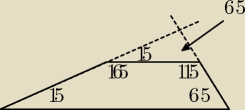
Saizou : a można tak to pokazać

Godzio: Tak trzeba

Rodney: a ja mam jeszcze pytanie odnosnie zadania 7, bo ja sobie to zrobilem wychodzac od: (2k−2)²+(2k)²+(2k+2)²+(2k+4)²=...=16(k²+k+1)+8 Dzięki temu minusowi miałem chyba odrobine prostsze obliczenia i zastanwiam sie czy np. na maturze byloby to bez problemow zaliczone? I jakie zalozenie trzeba w tym zadaniu napisac? k∊C czy k∊N ? No i czy liczby ujemne −2,−4,−6... tez uznajemy za parzyste?

Saizou : "Liczby parzyste to liczby całkowite podzielne przez 2. Każdą liczbę parzystą można zapisać w postaci 2k, gdzie k jest pewną liczbą całkowitą, np. −6, −4, −2, 0, 2, 4, 6, 8, 10, itd."

Godzio: Roodney zadanie jest dobrze zrobione, na resztę odpowiedział Saizou

Rodney: w sumie to zostaje do zrobienia chyba tylko to zadanie 6 z liczb rzeczywistych... wie ktos jak to zrobic?

Eta: Z nierówności między średnimi: am ≥gm

a   b   c   + + b   c   a		a		b		c
	≥ 3√		*		*		=1
3		b		c		a

	a		b		c
to:		+		+		≥3
	b		c		a

c.n.u

Rodney: Eta: gratuluje, zniszczylas mnie tym dowodem, kombinowalem cos ze srednimi od jakiegos czasu, ale na to nie wpadlem dziekuje bardzo