Kwadratowa! Taxi: W okrąg o promieniu R wpisano prostokąt o największym polu. Jaki prostokąt wpisano?

aniabb: https://matematykaszkolna.pl/forum/174072.html

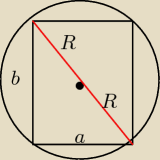
D'e: Teraz a² + b² = 4R² − Pan Pitagoras No i dostajemy a² = 4R² − b² (*) Pole prostokąta to a*b = b* √4R²−b² = √b²*(4R²−b²) Parabola w pierwiastku jest smutna zatem największą wartość osiągnie dla x wierzchołka F(x)=−b⁴+b²*4R² t = b² F(t)=−t² + t*4R² Największa wartość to będzie t=2R b²=2R ⇔b=√2R a więc (*) a²=4R²−2R² = 2R² ⇔a=√2R

Taxi: D'e a zro