wykaż że i prostokąt wpisany w okrąg rasputin: a) Wykaż, ze dla dowolnych liczb nieujemnych a i b spełniona jest nierówność

a+b
	≥√ab
2

b) W zbiorze prostokątów wpisanych w okrąg o promieniu R znajdź prostokąt o największym polu

dragon: a+b≥2√ab podnosimy stronami do kwadratu (można to zrobić bo obie str. są nieujemne)

rasputin: co do punktu b) mam jeszcze pytanie, czy zawsze, jeśli przecinamy prostokąt wzdłóż jego przekątnej, to kąty, które nam powstaną to będą : 90, 30 i 60 ?

Mila: a+b≥2√ab⇔ a−2√ab+b≥0 (√a−√b)²≥0 nierówność prawdziwa 2)

licealista: a nie trzeba pisać założenia że a≥0 i b ≥0

Mila:

	1
P=4*		R*R*sinα=2R2sinα
	2

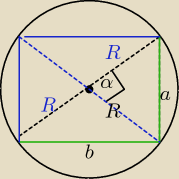
Największe pole dla sinα=1 ⇔α=90⁰ w takim razie dla kwadratu o przekątnych 2R a=b 2R=a√2

	2R
a=
	√2

rasputin: a zaraz, chyba, prostokąt może być kwadratem ? więc, tym prostokątem o największym polu będzie kwadrat? jeśli tak, to to będzie wyglądało w ten sposób : przekątna kwadratu wpisanego w ten okrąg to 2R potem z własności trójkąta (o kątach : 90,45,45) wychodzi mi, że bok tego kwadratu to R√2 , więc pole tego kwadratu / prostokąta o największym polu to : P = R√2 * R√2 = 2R²

Mila: Przecież to jest to samo co napisałam.

	2R		√2		2R√2
a=		*		=		=R√2
	√2		√2		2

Chciałam abyś sam usunął niewymierność. Ponadto, każdy kwadrat jest prostokątem.

Mila: Licealisto, piszesz założenia, bez założen nie można wyciągać pierwiastka kwadratowego z a, bo mogłoby być ujemne.