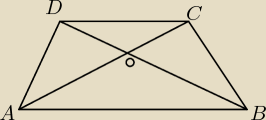
Kilka zadanej rozszerzonych Klementyna: Zad.1 Przekątne AC i BD trapezu ABCS o podstawach AB i CD przecinają się w punkcie O. Niech P trókjąta ABO = P₁ i P tr CDO = P₂ Udowodnij , że pole trapezu abcd jest kwadratem sumy pierwiastków P₁ i P₂ Zad2. Długoście boków trójkąta, którego jeden z kątów ma 120stopni są kolejnymi wyrazami ciągu arytmetycznego. Jaki jest stosunek boków tego trójkąta? Zad 3. Dana jest funkcja f(x)= |x|+|x−1| a) Udowodnij, że f(n); n∊N+ jest ciągiem arytmetycznym, a następnie ustal dla jakich n S₄=400 b)Zbadaj czy istnieje takie "a", że f(a+n)=f(a−4) Zad.4. Wyznacz równanie okręgu o środku s(10,−3), który jest styczny do prostej y=−3/4x +2 b) Wyznacz równanie stycznej do wyznaczonego okręgu, która jest prostopadła do danego punktu. Zad 5.Zaznacz na płaszczyźnie zbiór A={(x,y); x,y∊R 2x²−5xy+3y²≥0}. a następnie oblicz pole figury ograniczonej punktami (x,y) |y|=2 i |x|=3 Zad.6 Wiadomo , że f(x)=ax−3 jest f.rosnącą. Określ monotoniczność funkcji g(x)=f[2x−f(x)] w zależności od "a". Zad 7. W ostrosłupie, którego podstawą jest kwadrat ABCD o boku a, krawędź boczna DS jest prostopadła do pł ABCD, a |∡BSC|=∠. Oblicz Pc i V Z góry bardzo dziękuję za pomoc

Klementyna: podbijam

Mati_gg9225535: https://matematykaszkolna.pl/forum/158565.html

Klementyna: 2,3,6 jakoś zrobiłam Proszę o pomoc z 1,4,5.