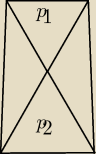
Oblicz pole trapezu, mając stosunek pól dwóch trójkątów, w nim zawartych. failedmission: Stosunek pól 2 trójkątów w trapezie wynosi 4/9. (p1 do p2). Oblicz pole trapezu.

failedmission: Jak się za to zabrać? Poproszę o wskazówki.

tad: ... trójkąty podobne ... k=?

failedmission: Co dla Ciebie oznacza litera "k"?

tad: skalę podobieństwa

failedmission: Czy mogę założyć, że suma pól tych dwóch trójkątów to połowa pola trapezu?

failedmission: Niestety nie potrafię wykorzystać skali prawdopodobieństwa do rozwiązania tego zadania. Rozumie, że mam znaleźć podstawy i wysokość trapezu i z tego obliczyć jego pole?

failedmission:

	2
k=		ale nie wiem do czego tego użyć.
	3

Mila: Zaraz zrobię.

Bogdan:

	P1		4
Jeśli dany jest tylko stosunek pól trójkątów:		=
	P2		9

to nie można obliczyć pola trapezu, potrzebne są jeszcze jakieś dane

failedmission: Też mi się wydaje, że bez dodatkowych danych nie da się tego rozwiązać.

tad:

25
	p2
9

failedmission: Mila mówi, że da radę rozwiązać więc cierpliwie czekam

failedmission: Tad możesz wyjaśnić jak Ci to wyszło?

tad:

	p1
... ale tu Bogdan ma racje ... nie znamy p2 ...tylko
	p2

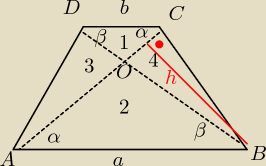
Mila: ΔABO∼ΔDCO − cecha kkk

b
	=k skala podobieństwa tych trójkątów
a

P1		4
	=
P2		9

Twierdzenie: Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa

P1		4
	=		=k2
P2		9

	2
k=
	3

ΔCOB i ΔDOA mają równe pola ( zastanów się dlaczego) OCA=2:3 (boki trójkątów podobnych są proporcjonalne)

	2
|OC|=		|OA|
	3

ΔCOB ma taką samą wysokość jak ΔBOA

	2
to P4=		P2
	3

	2
Ptrapezu=P1+P2+2*		P2
	3

	7
Ptrapezu=P1+		P2
	3

failedmission:

	25
Jak doszedłeś do tego, że Pole trapezu=		p2?
	9

failedmission: @Mila Dziękuję za wyjaśnienie.

Bogdan: Polecenie brzmi: "oblicz pole trapezu", a nie "wyznacz pole trapezu w zależności od P₁ lub P₂". Nie można w tym zadaniu obliczyć pola trapezu.

tad:

2   a+ a   3		2		5a		5		25ah2
	(h2+		h2)=		*		h2=
2		3		6		3		18

ah2		25
	=p2 .... po wstawieniu ...		p2
2		9

Mila:

tad:

	7		25
... Mila liczyła i liczyła ... i p1+		p2=		p2
	3		9

Mila: Można też wyrazić za pomocą P₁, ale ponieważ żadne nie jest dane...

Bogdan: Jeśli dane są pola P₁ i P₂, to pole trapezu można wyznaczyć z zależności: P_T = (√P₁ + √P₂)² Tu mamy tylko stosunek pól.

Mila: Wprawdzie nie wdaję się w utarczki słowne,lecz sprostuję: Tad objaśniałam, na kartce mam 1 linijkę.

tad: ... a do czegóż nam tu p₃ i p₄?

Bogdan: Wielokrotnie na forum był wyprowadzany wzór na pole trapezu w zależności od pól P₁ i P₂, m.in.: tu 56604

Mati_gg9225535: tak sobie analizowałem to zadanko i mam pytanie odnośnie rozwiązania Mili z daty _{8 paź 21:52}, skąd wiemy że "ΔCOB ma taką samą wysokość jak ΔBOA" ?

Artur ..... : ponieważ ich podstawy leżą na tej samej prostej (przekątna trapezu zawierająca punkty A,O,C) oraz wspólny wierzchołek z którego spuszczana jest wysokość (punkt B).

Mati_gg9225535: juz jasne

Mila: