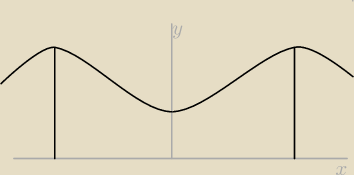
matematyka w zastosowaniach- konkurs- zadania przygotowujące Saizou : Słupy linii wysokiego napięcia stoją co 100 m. Jeśli dobrać układ współrzędnych jak na rysunku powyżej, to kształt linii odpowiada wykresowi funkcji y=c(10^kx+10^−kx). (Jest to tzw. katenoida, czyli krzywa łańcuchowa). Jaka powinna być wysokość słupów (z dokładnością do 1m), jeśli w najniższym miejscu kabel wisi 12 m nad ziemią, a 25 m dalej odległość kabla od ziemi wynosi 14,04m? bo mi wyszło 20m

Saizou :

aniabb: zależnie od przybliżenia ...ale chyba bliżej im do 21m

Saizou : bo ja to zrobiłem tak że f(0)=12 →c=12 dla funkcji kwadratowej o wzorze y=ax²+c f(25)=14,04 14,04=625a+12 2,04=625a a=0,003264 zatem wzór to f(x)=0,003264x²+12 wówczas f(50)=0,003264*2500+12=20,16m

Saizou : aniubb mogła byś sprawdzić

Saizou : up

aniabb: no to faktycznie 20 masz blizej ja to na piechotę w wolframie ćwiczyłam i nie chciało mi się dokładnie przepisywać

Saizou : dziękować

Saizou : Na osiedlu liczącym 100 domów firma ochroniarska monitoruje 50 domów inkasująca 80 zł miesięcznie od każdego obiektu. Dla zwiększenia przychodów ogłosiła akcję promocyjną: za każde dodatkowe 3 domy objęte monitoringiem zmniejsza opłatę o 2 zł miesięcznie. Jaki maksymalny przychód może uzyskać? Kiedy należy przerwać akcję promocyjną, by przychód już nie zmalał? i mi wychodzi że f(x)=(50+3x)(80−2x) dla x∊<0:16> x−trójka domów f(x)=−6x²+140x+4000

	−140
Xw=		≈12 zatem dla 36 dodatkowych domów przychód będzie największy
	−12

80*50=−6x²+140x+4000 0=x(−6x+140) x=0 x≈23 (sprzeczność z dziedziną), czyli akacja może objąć wszystkich

Saizou :

Saizou : up.

Saizou :

Joanna: https://matematykaszkolna.pl/forum/171563.html

Saizou : mógłby ktoś to sprawdzić

Saizou :

Saizou :

Saizou : czy mógłby ktoś to sprawdzić

Basia: to nie jest ani funkcja kwadratowa, ani parabola to jest katenoida wzór funkcji masz podany y=c(10^kx+10^−kx) najniższe miejsce odpowiada x=0 stąd 12 = c(10⁰+10⁰) = 2c c = 6 14,04 = 6(10^25k+10^−25k) z tego trzeba wyznaczyć k (wiesz jak ?) a potem policzyć f(100)

Saizou : a czy dla liny między słupami nie będzie to funkcja kwadratowa

Basia: Na osiedlu liczącym 100 domów firma ochroniarska monitoruje 50 domów inkasująca 80 zł miesięcznie od każdego obiektu. Dla zwiększenia przychodów ogłosiła akcję promocyjną: za każde dodatkowe 3 domy objęte monitoringiem zmniejsza opłatę o 2 zł miesięcznie. Jaki maksymalny przychód może uzyskać? Kiedy należy przerwać akcję promocyjną, by przychód już nie zmalał? a gdzie w Twoim wzorze przychód przy liczbie domów 51, 52, 54,55 itd. ? f(50) = 50*80 = 4000 f(51)=51*80 = 4080 f(52) = 52*80 = 4160 f(53) = 53*78 = ... f(54) = 54*78=... f(55) = 55*78=... f(56) = 56*76 =... jednym wzorem tej funkcji chyba nie da się opisać no chyba, żeby użyć entier f(50+x) = (50+x)*(80 − [^x₃]*2) x ∊{1,2,...,50} ale zbadać to będzie trudno albo takiej postaci f(50+3k) = (50+3k)*(80−2k) f(50+3k+1) = f(51+3k)= (51+3k)(80−2k) f(50+3k+2) = f(52+3k) = (52+3k)(80−2k) gdzie k=0,1,...,16 i trzeba badać te "gałęzie" oddzielnie a potem wybrać wartość naprawdę największą

Basia: ad.17:18 nie będzie, ona się przed słupem przegina

Saizou : ale przychód zmienia się co 3 domy więc tylko to warto uwzględnić (chyba)

katia: ∞∞∞

Basia: nie Saizu stawka zmienia się co trzy domy przychód zmienia się z każdym domem 50 domów ⇒ 50*80 = 4000 51 domów ⇒ 51*80 = 4080 22 domy ⇒ 52*80 = 4160 53 domy ⇒ 53*78 = 4134 54 domy ⇒ 54*78 = 4212 55 domów ⇒ 55*78 = 4290 56domów ⇒ 56*76 = 4256 i tak dalej...............