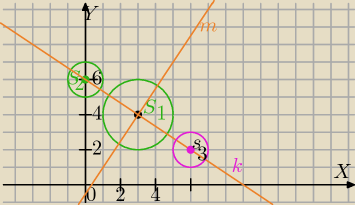
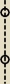 UWAGA TRUDNE, TYLKO DLA NAJLEPSZYCH ! na rysunku przedstawiono wzajmene położenie okręgów
o1(s1,2) i o2(s2,1)
a) narysuj trzeci okrąg o3 (s3,r3) taki, aby figura f będąca suma okręggów o1 o2 i o3 miała
środek symetrii. rozważ różne przypadki. w każdym z przypadków podaj długość promienia r3
b) wiedząc że okręgi o1 i o2 są określone odpowiednio równaniami (x−3)2+(y−4)2 i
x2+(y−6)2=1 napisz równanie okręgu o3 w każdym z przypadków.
c) napisz równania osi symetrii figury f
UWAGA TRUDNE, TYLKO DLA NAJLEPSZYCH ! na rysunku przedstawiono wzajmene położenie okręgów
o1(s1,2) i o2(s2,1)
a) narysuj trzeci okrąg o3 (s3,r3) taki, aby figura f będąca suma okręggów o1 o2 i o3 miała
środek symetrii. rozważ różne przypadki. w każdym z przypadków podaj długość promienia r3
b) wiedząc że okręgi o1 i o2 są określone odpowiednio równaniami (x−3)2+(y−4)2 i
x2+(y−6)2=1 napisz równanie okręgu o3 w każdym z przypadków.
c) napisz równania osi symetrii figury f
 Wszyscy pomagający potrafią zrobić.
Nie podałaś promienia pierwszego okręgu, ma być r=2?
(x−3)2+(y−4)2 =4
x2+(y−6)2=1
np.
S2S1→=[3,−2]
S1(3,4) →T→o wektor [3;−2]
otrzymujemy : S3=(3+3;4+(−2))=(6;2)
Figura złożona z tych 3 okręgów ma środek symetrii i 2 osie symetrii
S1 − środek symetrii
Wszyscy pomagający potrafią zrobić.
Nie podałaś promienia pierwszego okręgu, ma być r=2?
(x−3)2+(y−4)2 =4
x2+(y−6)2=1
np.
S2S1→=[3,−2]
S1(3,4) →T→o wektor [3;−2]
otrzymujemy : S3=(3+3;4+(−2))=(6;2)
Figura złożona z tych 3 okręgów ma środek symetrii i 2 osie symetrii
S1 − środek symetrii
| 2 | ||
k: y=− | x+6 Prosta przechodzi przez punkty (3;4) i (0;6) | |
| 3 |
| 3 | 3 | 1 | ||||
m:y= | x+b i 4= | *3+b⇔b=− | ||||
| 2 | 2 | 2 |
| 3 | 1 | |||
m: y= | x− | |||
| 2 | 2 |
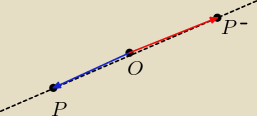 A umiesz rysować figury symetryczne względem punktu?
Zobacz przykład
O środek symetrii,
OP→ jest przeciwny do OP'→
P' jest symetryczny do punktu P względem p.O
Wektor [3;−2] jest przeciwny do wektora S1S2→ natomiast punkt S1 jest środkiem symetrii.
Zobacz na rysunek.
II przypadek
Punkt S2 to środek symetrii.
Teraz przesuwamy punkt S2 o wektor [−3;2] i to będzie środek okręgu o promieniu 2
A umiesz rysować figury symetryczne względem punktu?
Zobacz przykład
O środek symetrii,
OP→ jest przeciwny do OP'→
P' jest symetryczny do punktu P względem p.O
Wektor [3;−2] jest przeciwny do wektora S1S2→ natomiast punkt S1 jest środkiem symetrii.
Zobacz na rysunek.
II przypadek
Punkt S2 to środek symetrii.
Teraz przesuwamy punkt S2 o wektor [−3;2] i to będzie środek okręgu o promieniu 2