. asdf: Liczenie granicy z definicji:

	1
Udowodnij, że liczba 3, nie jest granicą ciągu an =		+ 1
	2n

	∃	∀
limn→∞ an = g ⇔			[ n > n0 ⇔ |an − g| <ε]
	ε>0	n0 ∊N

|a_n − g| < ε

	1
|		+ 1 − 3| < ε
	2n

	1
|		− 2| < ε
	2n

	1 − 4n
|		| < ε (wynika, że wartość jest < 0)
	2n

−1 + 4n
	< ε / * 2n (z def. n jest > 0)
2n

−1 + 4n < 2nε −1 < 2nε − 4n −1 < n(2ε − 4), teraz nawias musi być ≠0, czyli 2ε − 4 ≠ 0 ⇒ ε ≠ 2 Z definicji: Dla każdego dowolnie małego epsilona (ε > 0), a tutaj mam ε ≠ 2, więc jest sprzeczny z definicją, dobrze?

Trivial: https://matematykaszkolna.pl/forum/170580.html

asdf:

	2n
Wykazać na podstawie definicji, że granicą ciągu an =		jest liczba 2
	n + 3

	∃	∀
limn→∞ an = g ⇔			[ n > n0 ⇔ |an − g| <ε]
	ε>0	n0 ∊N

	2n
|		− 2| < ε
	n + 3

	2n− 2n − 6
|		| < ε
	n + 3

	−6
|		| < ε ( z def. będzie trzeba zmienić znak
	n + 3

6
	< ε
n+ 3

n + 3		1
	>
6		ε

	6
n + 3 >
	ε

	6
n >		− 3
	ε

Koniec? udowodnione?

Trivial: Udowodnione. Wystarczy wybrać n₀ = [6*¹_ε−3]+1.

asdf:

	1
Udowodnić, że g = 0 dla an = (		)n
	3

	1
|		n| < ε
	3

	1
|		|n < ε
	3

	1
(		)n < ε
	3

zamieniam na logarytm, pamiętając o znaku

	1
log1/3(		)n > log1/3ε
	3

n > log_1/3ε czyli za n₀ można przyjąć liczbę ≥ log_1/3ε

Trivial: za n₀ można przyjąć liczbę ≥ [log_1/3ε]+1

asdf: teraz mam takie coś w notatkach, czego nie rozumiem {E(log_1/3ε); log_1/3ε ≥ 1 n₀ { { 1 , log_1/3ε < 1 E(...) = całość z ...

Trivial: Racja. Dla małych wartości epsilon mamy ujemny jego logarytm, więc trzeba wybrać np. 1.

asdf: Tylko ja tego nie rozumiem

Trivial: Czyli w mojej wersji byłoby to:

	⎧	[log1/3ε]+1 dla ε≥ 1/3
n0 =	⎨
	⎩	1 w przeciwnym razie

Trivial: n₀ ma być naturalne, a liczby ujemne naturalnie naturalne nie są.

asdf:

	1
czyli n0 = 1 dla ε ∊ (0;		>? n0 = 1 bo to liczby naturalne i dlatego jest ta funkcja
	3

Atier?

b.: ad 27 lis 2012 21:26: wiersz 3: zamienione ∃ z ∀, oraz nie <=>, tylko => (!) (ten sam błąd jest później) wiersz przedostatni: −1 < n(2ε − 4), teraz nawias musi być ≠0, czyli 2ε − 4 ≠ 0 ⇒ ε ≠ 2 nawias nie musi być ≠0, przecież −1 < 0... więc niedobrze

asdf: @b. −1 < n(2ε − 4) n(2ε − 4) < 1 no a teraz masz sprzeczność, 0 < 1?

b.: jeśli chodzi o dobieranie n₀, nie rozumiem mody na wybieranie ,,konkretnego'' n₀, jak napiszesz tak jak napisałeś, że za n₀ można przyjąć liczbę [naturalną] ≥ log1/3ε (można dodać ,,naturalną'', ale to w zasadzie bez znaczenia), to jest to jak najbardziej poprawne.

b.: tylko że z tego, że −1 < n(2ε − 4) nie wynika, że n(2ε − 4) < 1 poza tym, 0<1 to nie sprzeczność

asdf: Możecie mi jeszcze odpowiedzieć na post z 21⁵²?

Trivial: 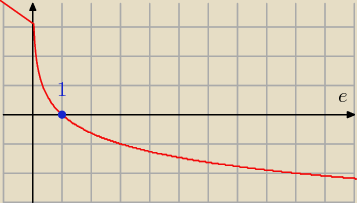asdf, wprowadziłem Cię w błąd. Zobacz na wykresie.

asdf: @b. Racja... To czemu wykładowca powiedział, że nie można dać takiego epsilona, np. ≠ 2 jak w tym przypadku ? Czy doktorek z 30 letnim doświadczeniem się pomylił?

asdf: @Trivial A mógłbyś mi to tak łopatologicznie wytłumaczyć po co akurat tutaj jest ta funkcja całość z...i te przedziały

Trivial: Jeżeli już wyznaczyć konkretne n₀ to masz: Dla ε < 1 log_1/3(ε) > 0 zatem podłoga będzie ≥ 0. Dla ε ≥ 1 log_1/3(ε) ≤ 0 zatem podłoga będzie ≤ 0. n₀ zerem być nie może, gdyż wtedy ciąg jest nieokreślony. Zatem wybieramy: Dla ε < 1: [log_1/3(ε)]+1, które jest zawsze ≥ 1 Dla ε ≥ 1: 1 (zobacz wykres)

asdf: jeszcze epsilon > 0 tak?

Trivial: Mimo wszystko, to co powiedział b jest jak najbardziej poprawne. Zawsze możesz napisać "wybieramy n₀ jako liczbę naturalną > log_1/3(ε)" i już.

Trivial: ε > 0 jest z założenia.

asdf: Tak łopatologicznie czytając:

	1
n0 będzie ...(i tu jakie?) dla przedziału od 0<ε ≤
	3

	1
a n0 będzie 1 ε ∊(		;∞)
	3

asdf: albo tak:

	1
n0 będzie zależało od epsilona, dla ε ∊ (0;		>, w przeciwnym wypadku n0 będzie równe 1
	3

	1
dla epsilona ∊ (		;∞), np.
	3

ε = 8 log_1/38 = −1,74564564(przybliżona wartość) A to, że jest to zbiór liczb naturalnych czyli n₀ zaczyna się od 1, CZYLI: Wszystkie wyrazy ciągu mieszczą się w pasku epsilonowym dla epsilona większego od 1/3, tak?

Trivial:

	1
To		było błędne. Powinno być 1.
	3

asdf: To już nie czaje....możesz mi to wytlumaczyc tak łopatologicznie jak w poscie z 22:18?

asdf: Co to jest ta podłoga?

Trivial:

	1
Po prostu		było błędne w moim poście z 21:50. Powinno być 1 (zobacz wykres).
	3

Zresztą... To jest tak nieistotna część tego zadania, że nie ma się nad czym rozczulać.

Trivial: Podłoga = część całkowita

asdf: Weź to powiedz mojemu wykładowcy..on mówi "jak liczycie to macie wiedzieć co".

b.: pierwszego zadania jeszcze nie poprawiłeś, ostatnie wnioski są błędne: akurat dla ε=2 wszystko jest OK

asdf: ostatnie wnioski to z 22¹⁸ W notatkach mam takie coś:

	1
Udowodnij, że g = 1 nie jest granicą ciągu an =
	n

	1
|		− 1| < ∊ (tego znaku bede uzywac)
	n

	1 − n
|		| < ∊
	n

−1 + n
	< ∊
n

−1 + n < ∊n −1 < en − n −1 < n(∊ − 1) n(∊ − 1) < 1 i tutaj mam taką notke; ∊≠ 1, w definicji: musi być on dowolnie większy od zera. w dodatku: nie można zrobić takiej rzeczy:

	−1
n >		( bo nie wiadomo czy nawias nie wyjdzie ujemny...
	∊ − 1

b.: i tutaj mam taką notke; ∊≠ 1, w definicji: musi być on dowolnie większy od zera. dlaczego ∊≠1? akurat taki ∊ jest (znowu) OK [ostatnia nierówność jest błędna, piszę niżej przedostatnią] teraz można tak: weźmy ∊=1/2, wtedy mamy −1 < n(1/2 − 1) −1 < −n/2 1 > n/2 2 > n nie ma takiego n₀, żeby dla n>n₀ zachodziło n<2

asdf: @b. Racja z tą nierównością, nie było wiele czasu na myślenie nad czym się pisze (wykładowca naprawdę szybko liczy)

asdf:

	3n + 2		3
Uzasadnij, że granicą ciągu		jest liczba
	5n − 1		5

	3n + 2		3
|		−		| < ∊
	5n − 1		5

	5*(3n + 2)		3(5n −1)
|		−		| < ∊
	5*(5n − 1)		5*(5n − 1)

	15n + 10 − 15n + 3
|		| < ∊
	25n − 5

	13
|		| < ∊ (widać, że wyrażenie pod w. bezw. jest > 0)
	25n − 5

13
	< ∊
25n − 5

25n − 5		1
	>
13		∊

	13
25n >		+ 5
	∊

	13   + 5 ∊
n >
	25

udowodnione?

Godzio: Ale Ty to rozumiesz czy mechanicznie robisz ? Co będzie jak dostaniesz nietypowy przykład np.

	n
		?
	2n

asdf: Ja to rozumiem tak, że:

	13
Jeżeli n0 > n, oraz n > (		+ 5 ) / 25 to każdy kolejny wyraz n0 znajduje się w
	epsilon

pasku epsilonowym, gdyby było takie coś: n < 1/epsilon itd.... to jest do pewnego wyrazu ciągu w epsilonie, a pozniej juz nie (czyli niezgodne z definicją) dobrze to rozumiem?

asdf: Jak mógłbyś to bardziej mi to wyjaśnij, bo się przyznaje, że do konca to tego nie rozumiem.

asdf: Inaczej...

	13   + 5 ∊		1
jeżeli n > n0, i n >		to dla dowolnie małego epsilona, np. ∊ =
	25		102

	13   + 5 1/102
n >
	25

n > 53,24 czyli n > n₀ to n₀ można przyjąć liczbę naturalną ≥ 53,24, czyli ≥54 Dla takiego przykładu jak wyjdzie:

	1
n <		, np. ∊ = 4/504
	2∊

	1
n <
	8/504

n < 63 czyli od pierwszego do 63 wyrazu ciągu będą w pasku, a kolejne już nie. Co jest niezgodne z definicją (dla dowolnie małego epsilona prawie wszystkie granice ciągu są w tym pasku − od n₀ do nieskończoności) dobrze?

asdf:

n
	. , granicą ciągu jest liczba 0
2n

teraz spróbuję to udowodnić:

	n
|		| < ∊ (opuszczam moduł, są dodatnie − z def ciągu)
	2n

n
	< ∊
2n

n
	< ∊
2n

2ⁿ < ∊ (znak ten sam, podstawa > 1) log₂2ⁿ <log₂∊ n < log₂∊ I teraz tak można:?

n
	> log2∊
log2∊

...nie chcę pisać bzdur

Artur_z_miasta_Neptuna: a niby dlaczego 2ⁿ < ε zresztą to nie ma sensu bo z założenia 2ⁿ to astronomicznie wielka liczba a ε to nieskończenie bliska 0 liczba

asdf: źle mnie zrozumiałeś. chciałem zamienić: 2ⁿ < ∊ na: n < log₂∊ i później dopiero napisałem:

n
	< log2∊
n

coś takiego wyjdzie? nie pasuje mi cos

Artur_z_miasta_Neptuna: a fuj fuj fuj samo napisanie 2ⁿ < ε jest już fuj i wszelkiego rodzaju zamiany nie mają najmniejszego sensu

asdf: więc jak rozwiązać tak banalny przykład?

Artur_z_miasta_Neptuna: musisz oszacować n <2^[n/2] <−−− możesz to np. szybko indukcyjnie wykazać, że jest to prawdą dla n>6 wtedy:

n		2[n/2]		1		1
	<		≤		<		= (*)
2n		2n		2[n/2]+1		2[N/2]+1

niech N = [2*log₂(1/ε)]

	1
(*) = 1/(2[log2(1/ε)] + 1) < 1/2log2(1/ε) =		= ε
	1   ε

c.n.w.

asdf: indukcji matematycznej nie miałem więc lipton...Ale dziękuję Spróbuję zrozumieć

Artur_z_miasta_Neptuna: tfu tfu tfu ...

2[n/2]		1
	≤
2n		2([n/2]−1)

oraz: niech N = [2*log2(1/ε)] + 4

Artur_z_miasta_Neptuna: asdf ... jak mogłeś skończyć liceum bez indukcji matematycznej

asdf: Musiałbyś się spytać nauczycieli albo ministerstwa edukacji A post 00⁰⁸ jest dobrze zrozumiane?

Artur_z_miasta_Neptuna: tok rozumowania prawidłowy ... ale wyliczeń wcześniejszych nie sprawdzałem

Artur_z_miasta_Neptuna: ale wydaje mi się (tak jak Godzilli ), że chyba nie rozumiesz do końca sposobu przeprowadzania dowodu istnienia granicy ciągu (korzystając z def Cauchy'ego) i robisz to trochę automatycznie

asdf: Zgodzę się, robię to trochę automatycznie, ale chyba też istotną sprawą jest to, że dopiero granicę ciągu miałem wczoraj i normalne jest to, że trzeba zrobić kilka(naście) przykładów żeby to dobrze zrozumieć Ja przynajmniej tak mam − robię − nie wiem co → odpuszcze na dzień−dwa, wrócę do tego i już coś zaczyna świecić w moim móżdżku

Godzio: 2ⁿ > n² dla n ≥ 5

n		n		1
	≤		=		< ε
2n		n2		n

	1
N = max{5,[		] + 1}
	ε

Artur też jestem tego zdania, że brak tu zrozumienia, a więcej idzie z automatu ...

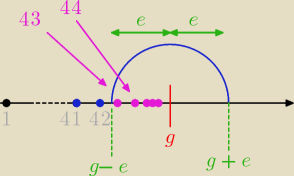
asdf: Napiszę tak jak to rozumiem (0 notatek, tylko z głowy), najwyżej sprawdźcie gdzie głupieje ok? Granicą ciągu nazywamy liczbę, do której zbiega ciąg, (n →∞), czyli im większy wyraz ciągu, tym bliżej granicy. Dla dowolnie małego epsilonika, znajdę taki wyraz ciągu, że kolejne wyrazu od tego wyrazu będą mieścić się w tym obszarze. |a_n − g| < ∊, czyli: a_n − g < ∊ → a_n < g + ∊ an − g > −∊ → a_n < g − ∊

	2
Taki przykład: udowodnić, że granicą ciągu an =		+ 1 jest liczba 1
	n

	2
|		+1 − 1| < ∊
	n

	2
|		| < ∊ (mogę opuścić moduł, bo z definicji, n ∊ N, czyli każda liczba dla n → ∞ będzie
	n

dodatnia.

2
	< ∊
n

można od razu taki trick:

	1		1
2 < 3, to		>
	2		3

n		1
	>
2		∊

	2		1
n >		, czyli wszystko się zgadza, bo ∊ > 0, na przykład dla ∊ =
	∊		21

	2
n >
	1   21

	21
n > 2 *
	1

n > 42 Czyli od n > 42 każdy kolejny wyraz mieści się w pasku epsilonowym.. Od wyrazu a₄₃ (nie można dać 42, bo 42 > 42...to logiczne, a n ∊ N, więc n=43). Każdy

	1
kolejny wyraz jest co raz bliżej granicy i nie bardziej oddalony od niej niż		) (na
	21

rysunku pokazane) W tym przypadku wyrazy ciągu nie osiągną wartości 1, ale są takie ciągi, gdzie osiągną i będą miały wartość większą od 1, a później do niej zbiegały). Jak wezmę jeszcze mniejszy epsilon to mniej wyrazów będzie znajdowało się w tym obszarze, ale i tak każde kolejne będą nadal zbiegać do granicy. P.S Jeżeli odległość od granicy dam ≥ 2 to cały ciąg będzie znajdować się w tym obszarze. Dobrze to rozumiem ?

asdf: .

aniabb: tak