trójkąty czy ktoś jest w stanie pomóc...: 1. W trójkącie prostokątnym ABC, w którym kąt ∡C = 90^o i BC < AC, poprowadzono prostą przez wierzchołek C trójkąta, która przecina przeciwprostokątną w punkcie D takim, że AD : DB = 2 :1 Oblicz długość przeciwprostokątnej, jeśli BC = √3 cm i ∡DCB = 30^o 2. W trójkącie dwa boki mają długość 12 cm i 3 cm, a kąt między nimi ma miarę 60^o. Oblicz: pole trójkąta długość promienia okręgu opisanego na tym trójkącie długość promienia okrędu wpisanego w ten trójkąt. 3. W trójkącie ABC, w którym AC = BC = 15 cm i ∡C = 30^o poprowadzono odcinek AD w ten sposób, że D ∊ BC oraz pole trójkąta ADC jest dwa razy większe od pola trójkąta ABD. Oblicz AD

Basia: Pomagam

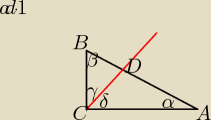
Basia: |BC| = √3 y=30 δ=90−30=60 β=90−α

|AD|
	=21
|BD|

|AD|=2*|BD| z tw.sinusów

sinγ		sinβ
	=
|BD|		|CD|

sinδ		sinα
	=
|AD|		|CD|

sin30		sin(90−α)
	=
|BD|		|CD|

sin60		sinα
	=
2*|BD|		|CD|

1		cosα
	=
2|BD|		|CD|

√3		sinα
	=
4|BD|		|CD|

|CD| = 2|BD|*cosα |CD|√3 = 4|BD|*sinα |CD| = 2|BD|*cosα

	4|BD|*sinα
|CD| =
	√3

	4|BD|*sinα
2|BD|*cosα=		/:2|BD|
	√3

	2sinα
cosα =
	√3

sin²α+cos²α = 1

	4sin2α
sin2α +		= 1 /*3
	3

3sin²α+4sin²α = 3 7sin²α = 3 sin²α = ³₇

	√3
sinα =
	√7

	|BC|
sinα =
	|AB|

√3		√3
	=
√7		|AB|

|AB|√3 = √3*√7 |AB| = √7

Basia: ad.2 a=3 b=12 γ=60 P = ¹₂*a*b*sinγ podstaw i policz c wylicz z tw.cosinusów

	c
R =
	2sinγ

	2P
r =
	a+b+c

Estrella: Ile powinno wyjść c, bo ja sie ciągle gubie w obliczeniach i mi nie wychodzi.

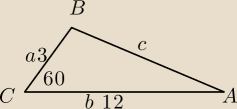
Mila: Zadanie 2) c²=3²+12²−2*3*12 *cos60

	1
c2=9+144−2*36*
	2

c²=153−36 c²=117 c=√117=√9*13 c=3√13 dalej poradzisz sobie?

bezendu: Mila to zadanie już było rozwiązane https://matematykaszkolna.pl/forum/210061.html ale ktoś tu je 3 razy wstawił dziś...