pola czworokatow
Agnieszka: W trapez równoramienny wpisano okrąg, którego średnica ma długość 8 cm. Obwód trapezu jest
równy 40 cm. Oblicz:
a) pole trapezu
b) długości boków trapezu
c) sinus kąta ostrego przecięcia przekątnych tego trapezu
Bardzo prosze o pomoc
21 lis 13:35
aniabb:
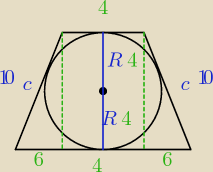
21 lis 13:39
aniabb:
trapez opisany a+b = c+c
obwód a+b+c+c=40
więc c+c+c+c=40 c=10
pitagoras 82 +x2 = 102 ⇒ x=6
a=x+b+x
a+b = 20
pole 20/2 * 8 = 80
boki 4,10, 16,10
21 lis 13:42
Agnieszka: A to jest jakas taka zasada ze a i b bd wynosic tyle samo co c i c?
21 lis 13:46
21 lis 13:47
Agnieszka: Bardzo dziekuje za pomoc

Potrafi ktos moze pomoc mi w podpunkcie "c"?
21 lis 13:52
Agnieszka: Na prawde sama nie wiem jak to nawet zaczac

a musze zaliczyc sprawdzian
21 lis 13:59
Artur_z_miasta_Neptuna:
zacznij od narysowania przekątnych
zauważ, że istnieje proporcja pomiędzy dolnym trójkątem (podstawa trapezu + części przekątnych
trapezu) z górnym trójkątem (górna podstawa trapezu + dalsze części przekątnych trapezu)
w ten sposób wyznacz wysokość trójkąta (dowolnego z tych dwóch)
i ze wzorów trygonometrycznych oblicz ∡(α/2)
21 lis 14:02
Agnieszka: widze ze ten trojkat u gory jest mniejszy ale jak mam zapisac ta zaleznosc?
21 lis 14:05
aniabb:
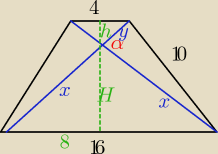
h/H = 4/16 ⇒H=4h
H+h = 8 5h=8 h = 1,6 H = 6,4
x
2=6,4
2+8
2 = ...
y=x/4
100 = x
2+y
2 − 2xycosα
sinα =
√1−cos2α
21 lis 14:06
aniabb: ale poszłam dookoła

czy w czworokątach środek okręgu wpisanego tez leży na dwusiecznych
21 lis 14:07

 Potrafi ktos moze pomoc mi w podpunkcie "c"?
Potrafi ktos moze pomoc mi w podpunkcie "c"?
 a musze zaliczyc sprawdzian
a musze zaliczyc sprawdzian
 h/H = 4/16 ⇒H=4h
H+h = 8 5h=8 h = 1,6 H = 6,4
x2=6,42+82 = ...
y=x/4
100 = x2+y2 − 2xycosα
sinα = √1−cos2α
h/H = 4/16 ⇒H=4h
H+h = 8 5h=8 h = 1,6 H = 6,4
x2=6,42+82 = ...
y=x/4
100 = x2+y2 − 2xycosα
sinα = √1−cos2α
 czy w czworokątach środek okręgu wpisanego tez leży na dwusiecznych
czy w czworokątach środek okręgu wpisanego tez leży na dwusiecznych