 spróbuje na pierwszym przykładzie rozpisać, dalej sam spróbujesz:
a) (m+1)x2 − 2(m−1)x +3m−3<0
oczywiście na początek dziedzina: x∊R
chcemy po lewej stronie otrzymać liczbę ZAWSZE mniejsza od zera żeby każda liczba x∊R spełniała
nierówność więc zajmijmy się tym warunkiem
Pierwsza opcja jest taka że równanie to będzie kwadratowe, gdy to co stoi przed x2 nie będzie
zerem, zatem mamy pierwszy warunek:
1) m+1≠0
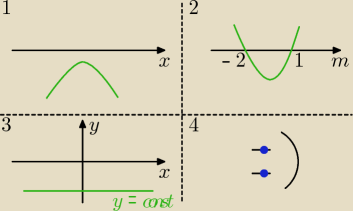
a teraz: kiedy wykres funkcji kwadratowej (parabola) leży pod wykresem osi OX ?
(patrz rys. 1)
otóż gdy nie ma miejsc zerowych (nie dotyka osi OX w żadnym punkcie) oraz gdy współczynnik a
jest ujemny (ramiona w dół)
mamy kolejne warunki:
2) Δ<0 (brak miejsc zerowych)
3) m+1<0 co w części wspólnej z pierwszym warunkiem daje właśnie trzeci warunek, zatem
zmieniamy pierwszy warunek do postaci trzeciego, trzeci wówczas jest zbędny
otrzymujemy dwa warunki które należy rozwiązać:
rozwiązujemy:
1) m+1 < 0
2) Δ < 0
1) m+1 < 0
m < −1
2) b2−4ac<0
[− 2(m−1)]2 − 4(m+1)(3m−3) < 0
4(m−1)2 −4*3(m+1)(m−1) < 0 (wyciągamy 3 przed nawias)
4(m2 − 2m + 1) − 12(m2−1) < 0 (pierwszy nawias podnosimy do kwadratu wg wzoru skróconego
mnożenia (a−b)2=a2−2ab+b2, drugi z trzecim łączymy korzystając ze wzoru skróconego mnożenia
(a−b)(a+b)=a2−b2)
4m2 − 8m + 4 −12m2 + 12 < 0
−8m2 − 8m + 16 < 0 (dzielimy obustronnie przez (−8) pamiętając o zmianie znaku
nierówności)
m2 + m − 2 > 0
liczymy Δ
Δ = 12 − 4*(−2)
Δ = 1 + 8 = 9
√Δ = 3
spróbuje na pierwszym przykładzie rozpisać, dalej sam spróbujesz:
a) (m+1)x2 − 2(m−1)x +3m−3<0
oczywiście na początek dziedzina: x∊R
chcemy po lewej stronie otrzymać liczbę ZAWSZE mniejsza od zera żeby każda liczba x∊R spełniała
nierówność więc zajmijmy się tym warunkiem
Pierwsza opcja jest taka że równanie to będzie kwadratowe, gdy to co stoi przed x2 nie będzie
zerem, zatem mamy pierwszy warunek:
1) m+1≠0
a teraz: kiedy wykres funkcji kwadratowej (parabola) leży pod wykresem osi OX ?
(patrz rys. 1)
otóż gdy nie ma miejsc zerowych (nie dotyka osi OX w żadnym punkcie) oraz gdy współczynnik a
jest ujemny (ramiona w dół)
mamy kolejne warunki:
2) Δ<0 (brak miejsc zerowych)
3) m+1<0 co w części wspólnej z pierwszym warunkiem daje właśnie trzeci warunek, zatem
zmieniamy pierwszy warunek do postaci trzeciego, trzeci wówczas jest zbędny
otrzymujemy dwa warunki które należy rozwiązać:
rozwiązujemy:
1) m+1 < 0
2) Δ < 0
1) m+1 < 0
m < −1
2) b2−4ac<0
[− 2(m−1)]2 − 4(m+1)(3m−3) < 0
4(m−1)2 −4*3(m+1)(m−1) < 0 (wyciągamy 3 przed nawias)
4(m2 − 2m + 1) − 12(m2−1) < 0 (pierwszy nawias podnosimy do kwadratu wg wzoru skróconego
mnożenia (a−b)2=a2−2ab+b2, drugi z trzecim łączymy korzystając ze wzoru skróconego mnożenia
(a−b)(a+b)=a2−b2)
4m2 − 8m + 4 −12m2 + 12 < 0
−8m2 − 8m + 16 < 0 (dzielimy obustronnie przez (−8) pamiętając o zmianie znaku
nierówności)
m2 + m − 2 > 0
liczymy Δ
Δ = 12 − 4*(−2)
Δ = 1 + 8 = 9
√Δ = 3
| −1+3 | −1−3 | |||
m1 = | m2 = | |||
| 2 | 2 |

 przyda mu się to gdy w zadaniu będzie miał inne polecenie
przyda mu się to gdy w zadaniu będzie miał inne polecenie 