Nierownosc
Jakub: Prosze o pomoc w rozwiazaniu nierownosci:
(x2 − 1)3 (x2 − 2x + 1) ≤0
16 lis 19:41
aniabb:
(x−1)5(x+1)3≤0
x∊<−1;1>
16 lis 19:46
Ajtek:
Zauważ że:
x2−1=(x+1)(x−1), zatem
(x+1)3(x−1)3(x−1)2≤0
(x+1)3(x−1)5≤0
16 lis 19:47
Ajtek:
Ja się tak nie bawię
Witaj
aniabb 
.
16 lis 19:48
Eta:
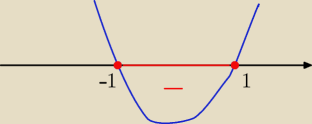
(x−1)
3*(x+1)
3*(x−1)
2≤0
(x−1)
5*(x+1)
3≤0 x=1 −−− pierwiastek pięciokrotny , x=1 −−− pierwiastek trzykrotny
x€<−1,1>
16 lis 19:48
Ajtek:
Witaj
Eta .
16 lis 19:48
aniabb:
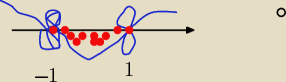
przecinasz oś tyle razy ile wynosi krotność
16 lis 19:49
Eta:
16 lis 19:49
Jakub: Dziękuje
16 lis 19:49
aniabb: i tak za wolno bo mi za pierwszym razem nie chciało narysować
16 lis 19:49
Eta:
A cóż to za "bohomaz" ? ( prezent Mikołajkowy?
16 lis 19:50
Jakub: A gdyby była parzysta krotność to odbiłoby się, tak?
16 lis 19:50
aniabb: Powiedzcie mi że te pętelki to mój pomysł
czy może ktoś to jeszcze stosuje
16 lis 19:50
aniabb: sposób na krotności..tyle razy przejeżdżam punkt do której potęgi jest nawias
16 lis 19:51
Ajtek:
Ja nie stosuje pętelek, można się zaplątać
16 lis 19:52
Eta:
16 lis 19:52
Jakub: A jak ugryźć to:
sin2(3x)=1
oraz
cos3x + sin2x − 3cosx + 2 > 0
16 lis 19:52
Saizou : ale ciekawy pomysł z pętelkami, pierwszy raz się z tym spotkałem, zawsze sobie tłumaczyłem że
jak jest parzysto−krotny pierwiastek od się odbija bo "parzy"
16 lis 19:53
aniabb: w drugim zamienić sin2x =1−cos2x i za cosx wstawić t
16 lis 19:54
Eta:
"parzysto− kopytny"
16 lis 19:54
Ajtek:
Do drugiego:
zauważ, że sin2x=1−cos2x
16 lis 19:54
aniabb: sin3x=1 lub sin3x=−1
3x=π/2 +2kπ lub 3x=3π/2 +2kπ
x=π/6 +2kπ lub x=π/2 +2kπ
16 lis 19:55
Ajtek:
"Człowiek jest parzystokopytny", tak koleżanka kiedyś napisałą na klasówce z biologii
16 lis 19:55
Saizou : sin
2(3x)=1
1−cos
2(3x)=1
cos
2(3x)=0
cos(3x)=0 3x=t
cost=0
16 lis 19:56
Jakub: czyli:
cos3x + 1 − cos2x − 3cosx + 2 > 0
A jak uporać sie z cos3 ?
16 lis 19:56
aniabb: pętelki wymyśliłam w technikum
potem życie sobie uprościłam..ale przypomniało mi się
16 lis 19:56
aniabb: no pisałam że podstawić t za cos
16 lis 19:57
aniabb: i pogrupować
16 lis 19:57
Eta:
2/(cosx−1)(cos2x+3)=0
cosx=1
x=.......
16 lis 19:58
Ajtek:
cosx=t podstaw i t∊<−1;1>
16 lis 19:58
Eta:
Po co Wam to "t" ?
16 lis 19:59
Trivial: aniabb, jak masz narysować (x−1)
100(x−2)
200 to też tak zapętlasz?
16 lis 20:00
aniabb: żeby widział wielomian a nie cosinusy
16 lis 20:01
Eta:
@
Trivial .......Dobre
16 lis 20:01
aniabb: chyba w technikum takich nie mieliśmy
a pętelki są takie logiczne
16 lis 20:02
Eta:
(x−1)
2013 i na maturze będzie 1h "zapętlania"
16 lis 20:03
Jakub: t3 − t2 −3t + 3 > 0
t2 (t − 1) − 3(t + 1) > 0 ?
16 lis 20:04
Eta:
Pierwiastek nieparzysto krotny ....... przechodzimy na drugą stronę
Pierwiastek parzysto krotny ............ odbijamy ( nie przechodzimy)
16 lis 20:05
aniabb: Eta..jak ja pisałam maturę było 5h na 3 zadania
mogłam sobie pozwolić
16 lis 20:05
16 lis 20:08
Eta:
W poście 19:58 chochlik powinno być
(cosx−1)(cos2x−3)>0
(cosx−1)(cosx−√3)(cosx+√3) >0
16 lis 20:09
16 lis 20:13
Jakub: A jak zabrac sie za to rownanie:
32x−1 − 2*(3)x−1 − 1 =0
16 lis 20:50
Jakub: Pomoże ktoś?
16 lis 20:58
aniabb:
3x=t
1/3 t2−2/3 t −1=0
delta
16 lis 21:01
Jakub: A inny sposob niz przez podstawienie?
16 lis 21:01
Ajtek:
| | 1 | | 1 | |
32x−1=32x*3−1=32x* |
| = |
| *32x |
| | 3 | | 3 | |
| | 1 | | 2 | |
2*3x−1=2*3x*U{3−1=2*3x* |
| = |
| *3x |
| | 3 | | 3 | |
Zatem:
3
x=t, t>0
Wiesz co dalej?
16 lis 21:03
aniabb: pisać cały czas 3
x zamiast t
16 lis 21:05
Jakub: Tak wiem, zresztą proszę o sprawdzenie:
t1 = −1
t2 = 3
16 lis 21:06
Jakub: Czyli t1 sprzeczne
16 lis 21:07
Jakub: Poprosiłbym jeszcze o pomoc albo sprawdzenie czy dobrze kombinuje z dziedzina:
√4−log1/22x
4−log
1/22x > 0
log
1/22x < 4
log
1/22x < log
1/22(−
√2)
16 lis 21:15
Ajtek:
I jeszcze 2x−2≠0
16 lis 21:17
b.: mam czapkę niewidkę
16 lis 21:18
Ajtek:
Tam jest log21/2x?
16 lis 21:18
Jakub: Tak, ale proszę powiedzieć czy dobrze rozwiazuje 1 zalozenie?
A jesli nie to prosze pokazac jak to powinno wygladac.
16 lis 21:19
Ajtek:
A ja mam magiczny proszek, cześć
b. .
16 lis 21:19
Jakub: log2 przy podstawie 1/2 z x
16 lis 21:20
ZKS:
log21/2x < 4 ⇒ −2 < log1/2x < 2
16 lis 21:22
Ajtek:
Nie.
log21/2x<4 /√
log1/2x<2 lub log1/2x>−2
16 lis 21:22
Jakub: Dziękuje
16 lis 21:27