trygonometria
Saizou : Witam wszystkich,
zaczynam powtórki z trygonometrii i liczę na waszą pomoc.
To może na początek jakieś zadanko

;>
PS. poziom rozszerzony LO
16 lis 16:17
Saizou : up
16 lis 16:55
funkcja: w moich postach jest trygonometria wiec prosze o pomoc.
16 lis 16:58
Mila: 1) 2cos
2x−5sinx=4 i x∊<0;2π>
2) α− kąt ostry
oblicz sinα+cosα
3) 4cos
2x=4sinx+1 i x∊<0;2π>
4) narysuj wykres funkcji
| | sin2x−|sinx| | |
f(x)= |
| dla x∊(0;π)∪(2π) |
| | sinx | |
sprawdzę po 20.
16 lis 16:59
Saizou : a może jakieś wkład własny
16 lis 17:00
Saizou : 1)
2(1−sin
2x)−5sinx−4=0
2−2sin
2x−5sinx−4=0
−2sin
x−5sinx−2=0 sinx=t, t∊<1:1>
−2t
2−5t−2=0
Δ=25−16=9
√Δ=3
| | 5+3 | |
t2= |
| =−2 sprzeczność |
| | −4 | |
16 lis 17:05
Saizou : 3) 4cos
2x=4sinx+1
4(1−sin
2x)−4sinx−1=0
4−4sin
2x−4sinx−1=0
−4sin
2x−4sinx+3=0 sinx=t , t∊<−1:1>
−4t
2−4t+3=0
Δ=16+48=64
√Δ=8
| | 4+8 | | 3 | |
t2= |
| =− |
| sprzeczność |
| | −8 | | 2 | |
16 lis 17:21
funkcja: 1. Prosta o równaniu y=3tg30ox tworzy z prosta o równaniu y=0 kat ostry o mierze :
2. Liczba sin17o * tg9o jest równa liczbie :
3. Liczba (sin1o + cos1o)2 :
A. nalezy do przedzialu (0; 120) B. nalezy do przedziału (120 ; 1) C. jest równa 1
D. jest większa od 1
Prosze to zadania z trygonometrii.
16 lis 17:22
Saizou :
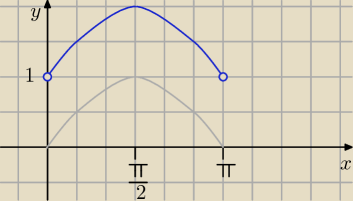
4)
zał: sinx≠0→x∉{0;π;2π}, czyli dziedzina to x∊(0:π), w tym przedziale sinus przyjmuje wartości
dodatnie, wówczas
| | sin2x−sinx | |
f(x)= |
| =sinx−1 (ta funkcja ma kolor niebieski) |
| | sinx | |
16 lis 17:30
Trivial: Dlaczego w górę przesunięte? Jest sin(x) − 1, czyli przesuwamy sin(x) o jeden do dołu.
16 lis 17:33
funkcja: a moje zadania ?
16 lis 17:34
Saizou : miało być w dół ale wykres lubi podróżować

16 lis 17:36
Saizou :
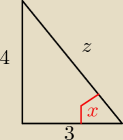
| | π | |
3) skoro x ∊(0: |
| ), mogę zrobić rysunek |
| | 2 | |
zatem z=5 (trójkąt pitagorejski)
wówczas
16 lis 17:36
Saizou :
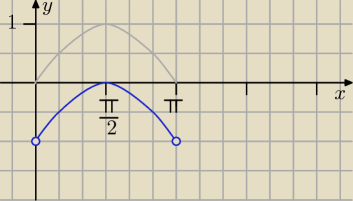
podróży ciąg dalszy
16 lis 17:42
Ajtek:
Tutaj Ciebie nie poratuję, zbiorek pożyczyłem

.
16 lis 19:40
Ajtek:
Witacie
Mila 
,
Trivial 
.
16 lis 19:41
Saizou : a szkoda, to czekam na inną dobrą 'duszyczkę'

16 lis 19:42
Trivial: Witaj.

16 lis 19:55
Ajtek:
Trivial, niestety nie mam pomysłu jak "pomalować" Twój nik u siebie

.
16 lis 19:56
Trivial: Ajtek, ja wszystkich maluję na czarno.

16 lis 19:57
Ajtek:
Aha

.
16 lis 19:59
aniabb: te o 17:22 zrobiłeś?
16 lis 20:10
Saizou : jeszcze nie
16 lis 20:15
Saizou : można prosić wskazówkę do 2
16 lis 20:22
aniabb: sądząc po dwukropku było coś do wyboru ... nie wiem do jakiej postaci chcieli
16 lis 20:24
Ajtek:
Do 3 chcesz podpowiedź?
16 lis 20:25
Saizou : 3 mam zrobione i 1
1) α=30
3)
(sin1+cos1)2=sin21+2sin1*cos1+2cos21=1+sin2 >1 bo sin2>0
16 lis 20:28
Ajtek:
Ja chciałem tylko podpowiedzieź, żebyś skorzystał ze wzoru skróconego mnożenia

.
16 lis 20:30
aniabb: 0,04631

16 lis 20:31
Saizou : a ja byłem cwany i wymnożyłem nawias przez nawias

(ale na serio użyłem wzorku)
16 lis 20:31
Ajtek:
Saizou 
.
16 lis 20:32
Saizou : no w sumie tak, przecież można z tablic odczytać
16 lis 20:32
Saizou : to ma ktoś jakieś zadanko
16 lis 20:42
Ajtek:
Sorry za offtop, ale mam pytanie.
Czy mogę znaleźć swój pierwszy post na tym forum. A jeżęli tak to w jaki sposób?
Przez szukajkę mi się nie udaje

.
16 lis 20:47
Saizou : niestety nie mam bladego pojęcia
16 lis 20:54
ZKS:
| | 3 | |
4tg2(x) − |
| * 41/2cos2(x) = −2 w przedziale x ∊ [0 ; 2π]. |
| | 2 | |
16 lis 20:55
Ajtek:
Cześć
ZKS 
.
16 lis 20:56
ZKS:
Witam
Ajtek.

16 lis 20:57
Ajtek:
Ależ kamuflaż

16 lis 20:58
ZKS:
Piotr mi pokazał ten kolor bo
Godzio go miał przez chwilę.

16 lis 21:00
Patryk: Przepraszam ze przeszkadzam ale czy w 17:22 w pierwszym nie bedzie 60 o ?
16 lis 21:01
Saizou : no niestety nie uczyłem się jeszcze o funkcji wykładniczej

16 lis 21:01
Saizou : | | √3 | |
tak będzie 60o bo 3* |
| =√3, a tgα=√3→α=60o |
| | 3 | |
16 lis 21:03
Patryk: grazie
16 lis 21:05
adaś: Ajtek może spróbuj wejść na ostatnią stronę na forum i nacisnąć znajdź i wpisać swój nick
,jeżeli o to
Tobie w ogóle chodzi.
16 lis 21:08
ZKS:
No to skoro tak to moje zadanie odpada chociaż tam jeżeli byś dobrze podstawił
to byś miał funkcje kwadratową.

16 lis 21:11
ZKS:
Poprawię zapis jeżeli ktoś będzie sobie rozwiązywał.

| | 3 | |
4tg2(x) − |
| * 41/(2cos2(x)) = −2 |
| | 2 | |
16 lis 21:14
Mila: Witaj, Ajtek, ZKS.
Ajtek szukałam Cię wczoraj, mogę zadać Ci pytanie?
Saizou, prosiłeś o zadania, wyszukałam i to jest mój wkład, ponadto obiecałam, że
sprawdzę.
W odpowiedziach pisz x=.. lub x=
Zadanie 2) na rysunku dajesz oznaczenie 3j , 4j ,5j (albo:3x,4x,5x gdzie x−wspólna miara)
zadanie 4)Wykres dokończ.brak wykresu dla x∊(π;2π)
16 lis 21:16
ZKS:
Witam
Mila.

16 lis 21:19
Saizou : Milu wielkie dzięki, co do wykresu to dałaś mi takie warunki x∊(0;π)∪(2π)
16 lis 21:19
Ajtek:
NIe było mnie wczoraj. Tzn może byłem ale nic nie pisałem

.
Jasne, że możesz

.
16 lis 21:23
PW: funkcjo, służę podpowiedzią do 2.Nie jest to takie trudne. Wystarczy zauważyć, że
45° − 9° = 36°.
Wartości funkcji trygonometrycznych kąta 36° są znane (znajdują się w tablicach, ale nie szukać
w tabeli przybliżonych wartości, lecz w tabelce pokazującej wartości dokładne dla niektórych
kątów).
Między innymi
tg36° =
√5 − 2√5.
Wiadomo, że
| | tgα−tgβ | |
tg(α−β) = |
| , |
| | 1+tgαtgβ | |
a więc
| | 1−tg9° | |
√5 − 2√5 = |
| |
| | 1+1tg9° | |
No to można powiedzieć, że tg9° mamy.
Dalej trzeba np. zauważyć, że tg60° = tg(3
.17°+9°).
Stąd można wyliczyć posługując się wzorem na sumę tangensów:
| | tg51°+tg9° | |
√3 = |
| . |
| | 1−tg51°tg9° | |
No to można powiedzieć, że mamy tg51°.
Posługując się wzorem na tangens potrojonego kąta dostaniemy
| | 3−tg217° | |
tg51° = tg17° |
| |
| | 1−3tg217° | |
Lewą stronę wyliczyliśmy (?) wcześniej, po prawej jest tylko niewiadoma tg17°, jeżeli potrafimy
rozwiązać to równanie, to znajdziemy tg17°, a więc i sin17°.
Koncepcja już jest, jeszcze tylko pół godziny uważnych rachunków i gotowe.
Może uda się komuś z większym talentem dobrać kąty i wzory, ale łatwiejszego sposobu nie ma.
16 lis 21:30
Ajtek:
Mila pytaj. Nie mogę się doczekać

.
16 lis 21:45
Mila: Do Ajtka
Mam pytanie o parking strzeżony w Warszawie, blisko Marszałkowskiej, gdzieś około 50 numeru.
Chodzi mi o to, aby nie zostawiać bardzo daleko auta na 2 dni.Pozdrawiam.
Saizou, oczywiście miało być dla x∊(0;π)∪(π;2π) =nieporozumienie.
16 lis 21:57
Ajtek:
No to mnie zabiłaś tym pytaniem

.
Zaczynam myśleć nad problemem

.
16 lis 21:59
Mila: Ajtek masz czas do wiosny.
16 lis 22:00
aniabb: Na środku placu konstytucji jest duży parking
16 lis 22:01
aniabb: to jest około 54 numeru
16 lis 22:02
Ajtek:
To jest rejon płatnego parkowania, dość rozległy, nawet bardzo rozległy

.
Dumam dalej
16 lis 22:04
aniabb: na placu defilad chyba był strzeżony..albo tylko dozorowany
16 lis 22:04
Ajtek:
aniabb ale tam wszystko jest płatne.
16 lis 22:05
aniabb: ale jak chce strzeżony to oczywiste że musi płacić
16 lis 22:07
Saizou :
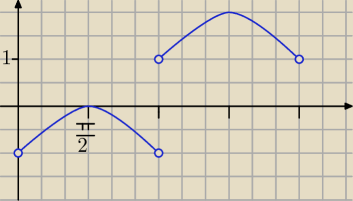
dla 0<x<π h(x)=sinx−1
dla π<x<2π g(x)=sinx+1
16 lis 22:07
aniabb: na placu powstańców był na 100% bo kiedyś parkowałam..ale nie wiem jaka jest teraz sytuacja jak
metro robią
16 lis 22:08
Ajtek:
Sorrry nie doczytałem
strzeżony 
.
16 lis 22:10
aniabb: ja na początku też jak proponowałam plac konstytucji
16 lis 22:14
Mila: Dziękuję Warszawiakom.Zapytam, jeszcze raz, gdy będę wyruszać do stolicy.

16 lis 22:14
Ajtek:
Podaj przyblizoną datę, zaokrąglij do miesięcy

16 lis 22:15
Mila: Kwiecień− koniec miesiąca.
16 lis 23:00
Ajtek:
Ok. przyjął do wiadomości.
W środku tygodnia czy weekend?
16 lis 23:06
Saizou : powrót do pierwotnego pytania:
ma ktoś zadana z trygonometrii poziom LO
17 lis 18:33
ZKS:
Podaj zbiór wartości funkcji:
f(x) = sin2(x)cos4(x)+sin4(x)cos2(x)
17 lis 18:50
aniabb: sprawdź tożsamość
| | sinα−sin3α+sin5α | |
1. |
| =tg3α |
| | cosα−cos3α+cos5α | |
2. 2(sin
6x+cos
6x)−3(sin
4x+cos
4x)+1=0
17 lis 19:05
Saizou : zadanie do
ZKS
sin
2xcos
4x+sin
4xcos
2x=sin
2xcos
2(cos
2+sin
2)=sin
2cos
2x=(sinxcosx)
2
| | 1 | |
sinxcosx, maksymalnie przyjmują wartość |
| , bo bo największą wartością jaką przyjmuje sinx |
| | 4 | |
| | √2 | | √2 | | √2 | | 1 | |
i cosx dla tego samego kąta to |
| , czyli |
| * |
| = |
| , a to |
| | 2 | | 2 | | 2 | | 2 | |
| | 1 | |
podniesione do kwadratu da |
| , |
| | 4 | |
17 lis 19:22
ZKS:
| | 1 | |
Saizou dobrze tylko mogłeś zauważyć że sin(x)cos(x) = |
| sin(2x) więc |
| | 2 | |
| | 1 | | 1 | |
( |
| sin(2x))2 = |
| sin 2(2x) a stąd już wszystko widać.  |
| | 2 | | 4 | |
17 lis 19:25
Saizou : może jakaś podpowiedź
17 lis 21:40
Saizou : sin
2+cos
2x=1 /
2
sin
4+2sin
2xcos
2+sin
4=1
sin
4+cos
4=1−2sin
2xcos
2x
sin
4x+cos
4=1−2cos
2x(1−cos
2x)
sin
4x+cos
4=1−2cos
2x+2cos
4x
sin
2x=1−cos
2x /
3
sin
6x=1−3cos
4x+3cos
2−cos
6x
sin
6x+cos
6x=1−3cosx
4+3cos
2
2(1−3cosx
4+3cos
2)−3(1−2cos
2x+2cos
4x)+1=
2−6cos
4x+6cos
2x−3+6cos
2x−6cos
4x+1=
−12cos
4+12cos
2x=
12cos
2(1−cos
2)=
12cos
2x*sin
2x=
3*(2cosxsinx)
2=
3(sin(2x))
2=3*sin
22x
i dalej nie wiem co

17 lis 22:45
Saizou : 
17 lis 22:53
Eta:
Ale o co chodzi? jaka treść zadania? ( bo nie wiem?

17 lis 23:06
Saizou : post aniibb z 19:05
17 lis 23:07
Eta:
zastosuj :
2/ a
6+b
6= (a
2+b
2)(a
4−a
2b
2+b
4)
i po ptokach

17 lis 23:14
Saizou : a dlaczego to nie chało wyjść moim sposobem

17 lis 23:16
Eta:
Też powinno, ale nie chce mi się sprawdzać, bo już ledwie na oczy widzę

17 lis 23:19
Saizou : już znalazłem błąd, siedział sobie tutaj
sin2x=1−cos2x /3
sin6x=1−3cos4x+3cos2−cos6x , a powinno być
sin6x=1−3cos2x+3cos4x−cos6x
17 lis 23:24
Eta:
No i "gitara"

17 lis 23:25
Saizou : 2(1−3cos2x+3cos4x)−3(1−2cos2x+2cos4x)+1=
2−6cos2x+6cos4x−3+6cos2x−6cos4x+1=0
L=P
17 lis 23:26
Eta:
Moim sposobem:
L=2(sin
2x+cos
2x)(sin
4x−sin
2x*cos
2x)−3sin
4x−3cos
4x+1=
= −(sin
4x+2sin
2x*cos
2x+cos
4x)+1= −(sin
2x+cos
2x)
2+1 = −1+1=0 =P

17 lis 23:29
Saizou : tak to jest jak się nie zna wzorków

17 lis 23:30
Eta:
Chochlik

tam w drugim nawiasie ( na początku) powinno być
( sin
4x−sin
2x*cos
2x+cos
4x)
17 lis 23:32
Eta:
Wniosek:
najwyższy czas je poznać 
17 lis 23:34
Saizou : lub też zacząć robić zadania z kartą wzorów

(chociaż ja ie lubię jej używać )
17 lis 23:37
Eta:
Dlaczego? .... "głowa nie śmietnik" ....i karta bardzo pomaga

17 lis 23:39
Saizou : ewentualnie używam jej do sprawdzania czy dobrze pamiętam wzory
17 lis 23:42
Eta:
A zad 2/ ?
| | 2sin3α*cos2α −sin3α | | sin3α(2cos2α−1) | |
L= |
| = |
| =tg3α |
| | 2cos3α*cos2α−cos3α | | cos3α(2cos2α−1) | |
L=P
17 lis 23:47
Saizou : nie było zrobione

17 lis 23:50
Eta: No to już jest !

17 lis 23:57
Saizou : to może jeszcze jakieś zadanko


18 lis 20:50
Saizou : up
18 lis 21:01
aniabb: sin3x(1+ctgx)+cos3(1+tgx)=cos2x
18 lis 21:10
aniabb: sin3x(1+ctgx)+cos3x(1+tgx)=cos2x
18 lis 21:11
aniabb: i na 100 tożsamość ...
| | sin(x+y+z) | |
tgx+tgy+tgz = |
| |
| | cosx + cosy + cosz | |
18 lis 21:15
Saizou : | | cosx | | sinx | |
L=sin3x+sin3x* |
| +cos3x+cos3* |
| = |
| | sinx | | cosx | |
=sin
3x+cos
3x+sin
2x*cosx+cos
2x*sinx=
=sin
3x+cos
3x+(1−cos
2x)cosx+(1−sin
2x)sinx=
=sin
3x+cos
3x+cosx−cos
3x+sinx−sin
3x=
=cosx+sinx
P=cos2x=cos
2x−sin
2=(cosx+sinx)(cosx−sinx)
L≠P
18 lis 21:18
aniabb: pierwsze to równanie..masz policzyć x

18 lis 21:20
Saizou : cosx+sinx=(cosx+sinx)(cosx−sinx)
(cosx+sinx)−(cosx+sinx)(cosx−sinx)=0
(cosx+sinx)(1−(cosx−sinx))=0
cosx=−sinx lub 1−cosx=sinx
| | π | | 3π | | π | |
x=− |
| +2kπ lub x= |
| +2kπ lub x=2kπ lub x= |
| +2kπ gdzie k∊C |
| | 4 | | 4 | | 2 | |
18 lis 21:26
Saizou : jak bym wiedział jak obliczyć sin(x+y+z) to był bym szczęśliwy

18 lis 21:28
aniabb: a dziedzina

18 lis 21:30
Saizou :
cosx+cosy+cosz≠0 i tu się pojawia problem
18 lis 21:31
aniabb: np ze wzoru na sumę sin((x+y) +z) i potem 2 raz
18 lis 21:31
aniabb: do poprzedniego dziedzina
18 lis 21:32
Saizou : a o tym to nie pomyślałem

18 lis 21:32
18 lis 21:33
Saizou : czyli 2 ostatnie odpowiedzi odpadają
18 lis 21:34
aniabb: a dlaczego −π/4
18 lis 21:46
Saizou : odpada bo dziedzina

18 lis 22:01
aniabb: a nie ..ok jest dobrze

18 lis 22:02
Saizou : nie wypada przecież
| | π | |
to jest − |
| =−45o a dziedzina jest 90ok |
| | 4 | |
18 lis 22:04
Eta:
A takie

Wykaż ,że dla kątów ostrych α,β,γ i α+β+γ= 90
o
| | α+β | | α+γ | | β+γ | |
zachodzi : cosα+cosβ+cosγ= 4cos |
| *cos |
| *cos |
| |
| | 2 | | 2 | | 2 | |
18 lis 22:19
19 lis 20:36
mika: potrzebuję zadanie z trygonometrii, akurat poziom rozszerzony LO

mogę liczyć na pomoc ? ;>
19 lis 20:59
Saizou : α=x
β=y
γ=z
x+y+z=90 i x,y,z są kątami ostrymi
| | x+y | | x+z | | y+x | |
cosx+cosy+cosx=4*cos |
| +*cos |
| *cos |
| |
| | 2 | | 2 | | 2 | |
| | x+y | | x+z | | y+x | |
P=4*cos |
| +*cos |
| *cos |
| = |
| | 2 | | 2 | | 2 | |
| | z | | y | | x | |
4*cos(45+ |
| )+*cos(45+ |
| )*cos(45+ |
| )= |
| | 2 | | 2 | | 2 | |
| | z | | z | | y | | y | |
4*(cos45*cos |
| +sin45*sin |
| )(cos45*cos |
| +sin45*sin |
| )(cos |
| | 2 | | 2 | | 2 | | 2 | |
| | x | | x | |
45*cos |
| +sin45*sin |
| )= |
| | 2 | | 2 | |
| | √2 | | z | | z | | y | | y | | x | | x | |
4*( |
| )3(cos |
| +sin |
| )(cos |
| +sin |
| )(cos |
| +sin |
| )= |
| | 2 | | 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
| | z | | z | | y | | y | | x | | x | |
√2(cos |
| +sin |
| )(cos |
| +sin |
| )(cos |
| +sin |
| ) |
| | 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
| | sinx | | siny | | sinz | |
L=cosx+cosy+cosz= |
| + |
| + |
| = |
| | cosx | | cosy | | cosz | |
| sinxcosy+cosxsiny | | sinz | | sin(x+y) | | sinz | |
| + |
| = |
| + |
| = |
| cosx*cosy | | cosz | | cosxcosy | | cosz | |
| sin(x+y)cosx+sinz(cosxcosy) | |
| |
| cosxcosycosz | |
i dalej nie mam pomysłu
21 lis 21:14
Eta:

21 lis 22:23
Godzio:
Moje zadanku sprzed dwóch lat !

21 lis 23:00
Eta:

21 lis 23:26
 ;>
PS. poziom rozszerzony LO
;>
PS. poziom rozszerzony LO
 4)
4)


 podróży ciąg dalszy
podróży ciąg dalszy
 .
.
 , Trivial
, Trivial  .
.


 .
.

 .
.
 .
.

 (ale na serio użyłem wzorku)
(ale na serio użyłem wzorku)
 .
.
 .
.
 .
.







 .
Jasne, że możesz
.
Jasne, że możesz  .
.
 .
.
 .
Zaczynam myśleć nad problemem
.
Zaczynam myśleć nad problemem  .
.
 .
Dumam dalej
.
Dumam dalej
 dla 0<x<π h(x)=sinx−1
dla π<x<2π g(x)=sinx+1
dla 0<x<π h(x)=sinx−1
dla π<x<2π g(x)=sinx+1
 .
.












 tam w drugim nawiasie ( na początku) powinno być
( sin4x−sin2x*cos2x+cos4x)
tam w drugim nawiasie ( na początku) powinno być
( sin4x−sin2x*cos2x+cos4x)

 (chociaż ja ie lubię jej używać )
(chociaż ja ie lubię jej używać )











 Wykaż ,że dla kątów ostrych α,β,γ i α+β+γ= 90o
Wykaż ,że dla kątów ostrych α,β,γ i α+β+γ= 90o
 http://www.cke.edu.pl/images/stories/Inf_mat_08/mat_informator_10.pdf na stronie 16 znajduje się co
"powinienem" umieć
http://www.cke.edu.pl/images/stories/Inf_mat_08/mat_informator_10.pdf na stronie 16 znajduje się co
"powinienem" umieć 
 mogę liczyć na pomoc ? ;>
mogę liczyć na pomoc ? ;>


