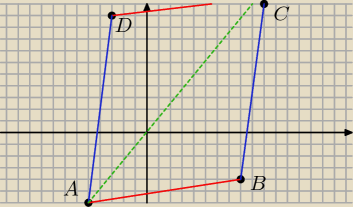
cześć ,potrzebuje pomocy z góry dzięki adrian2001: dane sa wierzchołki czworokąta A(−5,−6),B(8,−4) ,C(10,12), D(−3,10).Obicz obwód, pole otrzymanej figury oraz sprawdź czy ta figura jest trapezem . Znajdź równanie prostej zawierajacej przekątno AC

aniabb: obwód 2√173+4√65 Pole =204 tak jest trapezem ..proste AB i CD są równoległe a nawet równoległobokiem proste AD i BC też są równoległe prosta AC y=6/5 x

adrian2001: dzięki ajaki wzór zastosowałałeś na obwód

aniabb: https://matematykaszkolna.pl/strona/1248.html

Gustlik: Wektorami: A(−5,−6),B(8,−4) ,C(10,12), D(−3,10)

	2
AB→=[8−(−5), −4−(−6)]=[13, 2] ⇒ a1=
	13

	−2
CD→=[−3−10, 10−12]=[−13, −2] ⇒ a2=		=U{2]{13} ⇒ AB || CD ⇒ trapez
	−13

	16
BC→=[10−8, 12−(−4)]=[2, 16] ⇒ a3=		=8
	2

	16
AD→=[−3−(−5), 10−(−6)]=[2, 16] ⇒ a4=		=8 ⇒ AD || BC ⇒ równoległobok
	2

Wyznacznik wektorów: d(AB^→, AD^→= | 13 2 | | 2 16 | =13*16−2*2=204 Pole = |d(AB^→, AD^→|=204 (wzór na pole równoległoboku w układzie współrzędnych) Przekątna AC AC^→=[10−(−5), 12−(−6)]=[15, 18]

	18		6
a=		=
	15		5

	6
y=		x+b
	5

	6
12=		*10+b
	5

12=12+b b=0

	6
Odp: y=		x
	5