nierówność mesia666: −x³ −−−−−− >= 0 x−2

Kejt: pomnóż całość przez (x−2)² potem nie wymnażaj tylko napisz miejsca zerowe..a dalej przybliżony wykres i odczytujesz rozwiązanie.. w razie problemów, pytaj

altXOR:

−x3
	≥ 0 / *(x − 2)2
x − 2

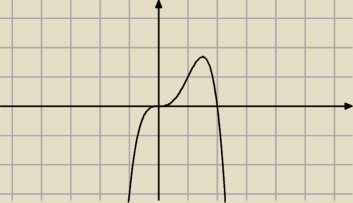
−x³(x − 2) ≥ 0 Jak widać −x³(x − 2) ≥ 0 ⇔ x ∊ <0, 2)

mesia666: no tak, tylko że mam wzór −x³(x−2)≥0 i jak się liczy m.z. jeśli jest potęga trzeciego stopnia

Kejt: normalnie.. traktujesz to na początku jak równanie: −x³(x−2)=0 czyli −x³=0 v x−2=0 i mamy miejsca zerowe 0 i 2..rozumiesz?

mesia666: dobra rozumiem, dzięki za pomoc tylko tam gdzie napisałeś czyli −x3=0 v x−2=0 powinno chyba być ∧

Kejt: napisałaś.. akurat w tym przypadku wg mnie jest to bez znaczenia czy użyje się 'i' czy 'lub'..

mesia666: "i" to jest, że obydwa wyrażenia są miejscami zerowym, a "lub" to jedno albo drugie także chyba jest różnica, ale najważniejsze że otrzymałem normalne wytłumaczenie a nie gotowe rozwiązanie, wielkie dzięki

Kejt: mądrala mnie zawsze uczyli lub, więc nie będę się kłócić

ICSP: jest różnica jednak z plusem dla Kejt

ZKS: Więc powinno być ∨ (lub) ponieważ to wyrażenie zeruje lub drugie nie muszą obydwa naraz zerować wyrażenia żeby było ∧ (i).

Kejt: yeah dzięki ICSP

ICSP: zawsze do usług

mesia666: niedobrze nie, dobrze oczywiście, że ktoś to wyjaśnił

Kejt: muszę sobie powtórzyć równania trygonometryczne..znalazłbyś czas/ chciałbyś mi potowarzyszyć?

ZKS:

Kejt: ZKS − wtapiasz się w tło niczym kameleon

ZKS: Ale nadal mnie widać niestety.

ZKS: Kejt jeżeli masz coś z równań trygonometrycznych to czy widziałaś to zadanie: sin(x) + cos(x) + 2sin(x)cos(x) = 1 jeżeli nie to rozwiąż sobie.

ICSP: Z tymi równaniami to było pytanie do mnie ?

Kejt: sinx + cosx + 2sinxcosx=sin²x+cos²x sinx+cosx=sin²x−2sinxcosx+cosx² sinx+cosx=(sinx−cosx)² w dobrą stronę...? czy niezbyt?

Kejt: oczywiście, że do Ciebie

ZKS: Też tak można.

Kejt: ok..na razie brak pomysłów na dalszą część..ale na razie..

ICSP: Ja nie mogę ale na pewno ZKS Ci pomoże z tym

Kejt: biedny ZKS

ZKS: A kto powiedział że nie możesz jeżeli chcesz to dawaj ICSP.

ZKS: Później Ci pokażę inny sposób Kejt.

ICSP: nie mogę Zakaz mam

Kejt: zakaz? od kogo? za co?

ICSP: od Godzia Powiedział ze prawie wszystko robię źle to lepiej żebym już nic nie robił

Saizou :

	π
czy to będzie x=−		+kπ, k∊C
	4

ZKS: Haha patrzcie jaki Godzio jest nie znałem go od tej strony.

Kejt: już ja sobie z nim porozmawiam.. Saizou..nie psuj

Saizou : ale to jest zła odpowiedź właśnie znalazłem błąd

ICSP: jutro go pomęczysz

ZKS: Saizou sprawdź sobie.

	1		1		1		1
−		+		+ 2 * (−		) *		= −1
	√2		√2		√2		√2

Kejt: dobrze..bo całą przyjemność z liczenia zabierasz.. jak to się mówi: "podanie odpowiedzi do zadania matematykowi jest jak przelecenie jego dziewczyny" tzn..w moim przypadku trochę inaczej, ale liczy się sens

Saizou : Kejt i jak idzie

ZKS: A Ty wreszcie zrobiłeś sobie Saizou?

Saizou : tak

Saizou : nawet ładne wyniki wychodzą

ICSP: ZKS pozwól ze wyjmę ciebie z ukrycia i się spytam : https://matematykaszkolna.pl/forum/166862.html Odp :

	1
sinx1/x * x1/x *		(lnx − 1)
	x2

Kejt: myślę..zapomniałam jak to się robiło

ZKS: Jeżeli zrobiłeś że cos^1/_x = e^{1/_xln(cos(x))} i teraz pochodna to .

ICSP: najpierw policzyłem ze złożenia a później dopiero policzyłem pochodną z x^1/x ale chyba to nie ma zbyt dużej różnicy?

ZKS:

	1		1		sin(x)
cos1/x(x) * [(−		2) * ln(cos(x)) +		* (−		)]
	x		x		cos(x)

ZKS: Saiozu jak wyszło to dobrze. A robiłeś tym samym sposobem co Kejt?

Saizou : trochę innym, ale wynik jest OK

ZKS: ICSP właśnie ciekawe jak tam jest czy (cos(x))^1/_x czy cos(x^1/_x).

ZKS: Jak Kejt zrobi to możesz pokazać jakim sposobem.

Saizou : ja jeszcze tylko będę 30 min, bo muszę jutro wcześnie wstać niestety

Saizou : mogę dać podpowiedź

ZKS: No podaj podpowiedź dla Kejt.