geometira Madzia: Wewnątrz kwadratu ABCD Wybierzmy punkt X taki, aby trójkąt CDX był trójkątem równoramiennym, którego kąty przy wierzchołkach C i D mają taką samą miarę 15^o. Co można powiedzieć o trójkącie ABX?

Bogdan: 166639

Basia: 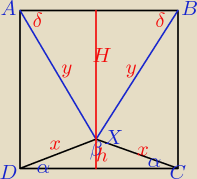ABX jest na pewno równoramienny trzeba by chyba znaleźć kąt δ a na to są różne sposoby:

	a2
cos15 =
	x

	a
x =
	2cos15

albo z tw. cosinusów a² = x²+x²−2x*x*cos(150)

	√3
a2 = 2x2 + 2x2*
	2

	√3
a2 = 2x2(1+		}
	2

	2+√3
a2 = 2x2*
	2

a² = x²*(2+√3)

	a2		a2(2−√3)
x2 =		=		= a2(2−√3)
	2+√3		1

teraz z tr.DXA i tw.cosinusów można wyliczyć y y² = a²+x² − 2ax*cos75

	a2		a
y2 = a2+		−2a*		*cos75
	4cos215		2cos15

to się jak sądzę da uprościć (pokombinuj)

	a2
a mając y można wyliczyć cosδ=
	y

i dowiedzieć się jakim kątem jest δ