równanie kierunkowe dorota: wyznacz równanie kierunkowe prostej AB, jeśli A=(−1,1),B=(2,−1). następnie wyznacz punkty przecięcia tej prostej z osiami współrzędnych.

aniabb: https://matematykaszkolna.pl/strona/1223.html

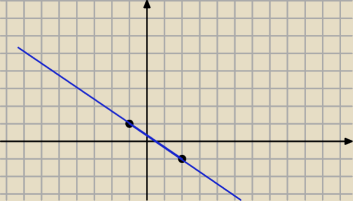
aniabb: y=−2/3 x +1/3 0Y to (0;1/3) 0X to (1/2;0)

dorota: dziękuję

Gustlik: Wektorami: A=(−1,1) B=(2,−1) AB^→=[2−(−1), −1−1]=[3, −2]

	−2		2
a=		=−
	3		3

	2
y=−		x+b
	3

	2
1=−		*(−1)+b
	3

	2
1=		+b
	3

	1
b=
	3

	2		1
y=−		x+
	3		3

OX: miejsce zerowe funkcji liniowej:

	2		1
−		x+		=0 /*3
	3		3

−2x+1=0 −2x=−1 /:(−2)

	1
x=
	2

	1
P=(		, 0)
	2

	1
OY: (0, b)=(0,		)
	3

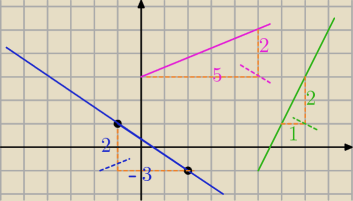aniabb: zamiast tak dziwnie brzmiąco "wektorami" to po prostu liczę kratki np.: niebieskie 3do tyłu 2 w górę dopisuję kreskę ułamkową i mam a=−2/3 zielona 1 do przodu 2 w górę kreska i mam a=2/1 = 2 fioletowa y=2/5x +3 (wyraz wolny z przecięcia z osią 0Y )

Gustlik: aniabb wektory nie są niczym dziwnym, to podstawa geometrii analitycznej, znacznie ułatwiają życie. Pozdrawiam.

Gustlik: [B[aniabb twoja metoda jest też fajna, w sumie wynika ona ze "schodkowej" metody rysowania wykresów funkcji liniowej opisanej tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=41 .

aniabb: że wektory są podstawą to ja wiem... ale zazwyczaj zadania tłumaczę pięknym niebieskookim blondynkom którym idealnie wychodzi liczenie pazurków do pomalowania