log
iza: pomóżcie
logx343=3/2
9 lis 18:22
Piotr:
x3/2 = 343
9 lis 18:23
iza: tak ale ile wynosi x
9 lis 18:26
iza: i jak dojść do tego?
9 lis 18:26
Piotr:
podnies obustronnie do potegi 2/3
9 lis 18:27
aniabb: x= (3√343)2
9 lis 18:28
iza: napiszecie mi to krok po kroku?
9 lis 18:31
Piotr:
ale to juz wszystko.
x = 3432/3
x = (3√343)2
x = 72
x = 49
9 lis 18:33
iza: dzieki
9 lis 18:35
iza: juz rozumiem
9 lis 18:35
Piotr:
9 lis 18:39
Eta:
Można też tak: 343= 7
3
log
x7
3 = 3log
x7
| | 3 | | 1 | |
3logx7= |
| ⇒ logx7= |
| ⇒ x= 49 |
| | 2 | | 2 | |
9 lis 18:42
iza: mam problem
log2(x2−10x+9)=1
9 lis 18:43
MQ: x2−10x+9=21
9 lis 18:45
Eta:
założenie x2−10x+9 > 0 ⇒ (x−1)(x−9)>0 x€ ............
z def. logarytmu x2−10x+9 = 21 ⇒ x2−10x +7=0 ...... dokończ
pamiętaj o założeniu
9 lis 18:46
Piotr:
i x2−10x+9 > 0
9 lis 18:46
MQ: Nie trzeba dawać, sierotki, założenia, bo sama treść zadania zapewnia jego
spełnienie.
9 lis 18:48
Eta:
@[PMQ]] ........"sierotek" poszukaj w rodzinie
9 lis 18:51
Piotr:
witaj
Eta spokojnie
MQ wyjasnilbys mi ?
9 lis 18:53
iza: obliczm delte tak? ale wychodzi mi x1=1,52 a x2=9,24 dobrze? czyli sa 2 rozw.?
9 lis 18:53
Piotr:
x1 = 5 − 3√2
x2 = 5 + 3√2
9 lis 19:07
iza: nie wiem skad to sie wzielo moglbys rozpisac? proszę
9 lis 19:08
Piotr:
Δ = 100 − 28 = 72
√Δ =
√72 =
√36*2 = 6
√2
| | 10−6√2 | | 2(5−3√2) | |
x1 = |
| = |
| = 5 − 3√2 |
| | 2 | | 2 | |
x
2 podobnie tylko z plusem
prosze
9 lis 19:11
iza: dzieki bardzo
9 lis 19:12
MQ: @Piotr
Skoro z treści zadania wynika, że:
x2−10x+9=21
To oczywiste jest, że wynik zapewnia:
x2−10x+9>0, bo 21>0
Sorry za obsuwę w czasie, ale zrobiłem sobie przerwę na "1z10".
9 lis 19:23
iza: czy mozecie luknąc czy dobrze licze;
log(3√3)27 to rowna sie 2
log(1/√3)27=−6
9 lis 19:31
9 lis 19:34
iza: a moglbys napiac jak to robisz?
9 lis 19:36
MQ: | | log√327 | | log√3√38 | | 8 | |
log3√327= |
| = |
| = |
| |
| | log√33√3 | | log√3√33 | | 3 | |
i analogicznie drugie
9 lis 19:39
iza: skoro tamto zle mi wyszlo tp jak mam policzyc to bo nie mam pomyslu:(
log(√3/√2)8/27 w podstawie √3/√2
9 lis 19:39
MQ: Przepraszam, ty miałaś dobrze, bo 27 to √36
9 lis 19:45
iza: ale nie rozumiem dlaczego dzielisz przez log√33√3
nie mozna tego tak zrobic log3√327=x i nastepnie (3√3)x=27
9 lis 19:45
MQ: 
9 lis 19:46
MQ: Można oczywiście.
9 lis 19:47
iza: ja czy ty
haha
9 lis 19:48
iza: nio to ciesze sie bo mam problemy z matma i kazde dobrze zrobione zad to sukces
9 lis 19:49
MQ: No oczywiście ja
9 lis 19:49
iza: pomozesz z tym log(√3/√2)8/27
9 lis 19:49
iza: to zwykla pomylka tylko nie przejmuj sie
kazdemu sie zdaza
9 lis 19:50
MQ: więc log... itd będzie=−6
9 lis 19:52
iza: nie wazne ze sa inne podst. pierw.?
9 lis 19:55
iza: potegi sorrki
9 lis 19:55
MQ: Przecież potęgi są jednakowe:
8=√26
27=√36
9 lis 19:57
iza: ale mamy w przykladzie log(√3/√2)8/27=x i ja robie to tak (√3/√2)x= ((√2)/(√3))6
9 lis 20:01
MQ: No, (√3/√2)x=8/27=(√2/√3)6=(√3/√2)−6
stąd
x=−6
9 lis 20:06
iza: pomocy czy z tego logx9+1/2logx16=2 wyjdzie 3,46
9 lis 20:06
iza: aha zamieniles lcznk z mianownikiem kumam juz
9 lis 20:07
MQ: Pisz porządnie:
Czy to jest?
9 lis 20:08
Piotr:
nie
9 lis 20:08
Piotr:
nie bylo do tego, ze nie wyjdzie 3,46
9 lis 20:09
iza: tak, sorki pierwszy raz jestem tu nie wiem dokladnie jak pisac te znaki rozne:(
9 lis 20:09
9 lis 20:10
iza: dzieki
9 lis 20:11
Piotr:
logx9 + logx4 = 2
logx36 = 2
poradzisz sobie ?
9 lis 20:14
9 lis 20:15
iza: tak
9 lis 20:17
iza: dzieki, a taki przyklad 2x−4=(√2)2−3x to bedzie U{5}/{4}
9 lis 20:24
MQ: Mi wyszło x=2, ale, jak wiesz, lubię się mylić.
9 lis 20:28
iza: jejku to znow zle mam jak to zrobiles?:(
9 lis 20:29
Piotr:
wychodzi 2
√2 = 2
1/2
9 lis 20:29
MQ: W tym wypadku prościej przyjąć 2=√22
9 lis 20:30
iza: juz wiem co mam zle:( ale gapa jestem
9 lis 20:30
iza: ja zrobilam jak Piotr tylko w mnozeniu sie pomylilam:(
9 lis 20:31
9 lis 20:33
Piotr:
bez roznicy, musi wyjsc to samo.
9 lis 20:33
iza: tak wyszlo 2
9 lis 20:34
9 lis 20:34
Piotr:
podstawa jest 10 ?
9 lis 20:34
iza: tak i wyszlo mi 500000 czy to dobrze
9 lis 20:35
Piotr:
5*10
5
9 lis 20:37
iza: musze korzystac z tego wzoru bo gubie sie jak robie z tego wzoru a do mojego wyniku doszlam
9 lis 20:37
iza: to zle
?
9 lis 20:37
Piotr:
dobrze
to to samo
9 lis 20:38
iza: uffff
9 lis 20:39
Piotr:
przeciez mozesz sobie sprawdzic
| | 5*105 | |
log |
| = log 10 5 = 5  |
| | 5 | |
9 lis 20:40
iza: a w tym przykladzie najpierw licze log osobno a poznej podkladam?
loglog23=2log23{x+2}
9 lis 20:41
Piotr:
dobrze przepisane ?
9 lis 20:44
iza: oj pomylka tam powinno byc na poczatku zamiast log 4
9 lis 20:45
iza: sorrrki
9 lis 20:45
Piotr:
to przepisz cale jeszcze raz
9 lis 20:45
iza: 4log23=2log23{x=2}
9 lis 20:47
Eta:
4log23= 2log23(x+2)
9 lis 20:47
9 lis 20:48
iza: 4log23=2log23{x+2}
9 lis 20:48
Piotr:
używaj tam nawiasów okrągłych bo niewiadomo czy nie chodzilo o cos innego.
9 lis 20:49
Piotr:
poradzisz sobie z zadaniem ?
9 lis 20:50
iza: oki
wychodzi mi zle chyba bo 0:(
wiec tak robie
2*3=3(x+2)
9 lis 20:54
Piotr:
nie, nie
po lewej bedziesz miec 32 czyli 9.
2log23 = log232 = log29
9 lis 20:56
Piotr:
dziedzina x+2 > 0 ⇒ x > −2
9 lis 20:58
iza: odp.1?
9 lis 21:06
Piotr:
9 lis 21:07
iza: dzieki
9 lis 21:07
iza: 2log(2−x)−logx=log(x−5) co mam zrobic z log po znaku =
9 lis 21:12
Piotr:
po pierwsze dziedzina. mam nadzieje ze wiesz jak
korzystasz tylko ze wzorow.
log(2−x)
2−logx=log(x−5)
9 lis 21:17
Piotr:
sprawdz czy dobrze przepisane bo wychodzi mi brak rozwiazan.
9 lis 21:24
iza: dziedzina z nawiasów tak
9 lis 21:31
iza: bląd sorki tam jest x+5
9 lis 21:32
Piotr:
proszę sprawdz czy dobrze przepisalas zadanie, dokladnie
i pokaz jak liczylas dziedzine.
9 lis 21:33
Piotr:
to duzo zmienia. jest rozwiazanie
9 lis 21:34
iza: 2log(2−x)−logx=log(x+5)
2−x>o
x>2
x+5>0
x>−5
9 lis 21:36
iza: x=1
9 lis 21:39
iza: nie x=−1/3
9 lis 21:40
Piotr:
źle policzylas.
2−x > 0
−x > −2 //*(−1)
x < 2
i x>0
i x> − 5
i teraz czesc wspolna
9 lis 21:40
iza:
9 lis 21:40
Piotr:
najpierw wyznacz dziedzina. a rownanie rozwiazujesz takie jak pisalem wyzej tylko po prawej
bedzie x + 5
9 lis 21:41
iza: od −5 do 2
9 lis 21:41
Piotr:
moj post z 21:40 dotyczy dziedziny. trzeba ja wyznaczyc.
9 lis 21:42
Piotr:
źle
narysuj sobie na osi x>0, x> −5, x<2
9 lis 21:43
iza: D:xnalezy(−5,2)
9 lis 21:45
Piotr:
nie. x ∊ (0 ; 2)
9 lis 21:46
iza: D:xnalezy (−nieskonczonośc,2)
9 lis 21:46
iza: ale jestem tepa:(
9 lis 21:47
Piotr:
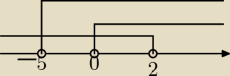
widzisz gdzie jest czesc wspolna ?
9 lis 21:49
iza: tak juz sobie narysowalm i zauwazylam juz to, ale dzieki wielkie,bardzo dziekuje ze masz do
mnie cierpliwosc.
9 lis 21:51
iza: a sluchaj jak tam zmnienia sie ten znak −x>−2 na x<2 to zawsze tak jest jak mnozymy pzrez −1
9 lis 21:52
Piotr:
mozesz podzielic przez −1
bez różnicy.
9 lis 21:58
iza: ale znak zmieniam jak mam po obu str minus?
9 lis 21:58
9 lis 21:59
Piotr:
9 lis 22:01
Piotr:
zmieniasz znak gdy mnozysz lub dzielisz przez liczbe ujemna.
9 lis 22:02
iza: naprawde
?
9 lis 22:02
Piotr:
tak
9 lis 22:03
iza:
9 lis 22:05
iza: dzieki
9 lis 22:06
Piotr:
mam nadzieje, ze pomoglem
9 lis 22:07
iza: bardzo, nawet nie wiesz jak jestem dłużniczką
9 lis 22:08
Piotr:
9 lis 22:09
iza: moge jeszcze troszke Cie pomeczyc
plisss
9 lis 22:11
iza: | | logx | |
mam taki przyklad |
| =−1 |
| | log(x+1) | |
9 lis 22:12
iza: robie z tego roznice? i co dalej
9 lis 22:13
iza: czy skracam log znaczy pomijam?
9 lis 22:14
Piotr:
nie ma takiego wzoru
spojrz jeszcze taz na ten wzor o ktorym myslisz.
jakie bys dala zalozenia do dziedziny ?
9 lis 22:16
iza: Z:x>0
9 lis 22:18
Piotr:
nie. napisze Ci wszystkie zalozenia :
x>0
x+1>0
log(x+1)≠0
9 lis 22:19
Piotr:
w sumie wyjdzie x>0
9 lis 22:21
iza: czyli co dobrze to zalozenie moje?
9 lis 22:21
Piotr:
nie no moje zalozenia sa dobre i ich czesc wspolna to x>0
9 lis 22:22
iza: jejku ja sie zastrzelę przez ta matme, a jeszcze na gorze u mnie impre sobie robia
porazka
9 lis 22:22
Piotr:
a co do rownania to pomnoz przez mianownik.
9 lis 22:23
iza: ojjjj zlituj sie ale gdybym napisala tylko x>o to byloby zle? musze odniesc sie do wszystkich x
a pozniej D to czesc wspolna tak?
9 lis 22:23
iza: czyli moje pomysly byly zle:?
9 lis 22:24
iza: D to 0, + nieskon
9 lis 22:25
Piotr:
do dziedziny : tak, trzeba wszystkie zalozenia wypisac i obliczyc i czesc wspolna jest
dziedzina.
co do rownania : juz pisalem, ze nie ma takiego wzoru wiec Twoje pomysly niestety zle .
9 lis 22:26
iza: ale ta D to −1,0 czy 0, +nieskon
9 lis 22:27
Piotr:
tak, D: x ∊ (0; +
∞)
PS znaczki
∞ ≤ ∊ masz nad polem do wpisywania tekstu
9 lis 22:27
iza: kiedy pisze na nieskon
9 lis 22:27
iza: dzieki:(( ale masz polewke ze mnie co
bieda
9 lis 22:28
Piotr:
jak kiedy ? kiedy tak wychodzi. wyszlo x>0 czyli nie ma gornej granicy wiec x ∊ (0; +∞)
9 lis 22:29
iza: a co z tym −1
9 lis 22:30
Piotr:
zadnej polewki nie mam. widze, ze sie starasz. i bardzo dobrze !
do dziela z tym rownaniem
9 lis 22:30
iza: dzieki naprawde wporzadku jestes bardzo wporzadku.
9 lis 22:31
Piotr:
x+1>0
x> −1 czyli czesc wspolna x>0 ( narysuj sobie os jak nie widzisz)
9 lis 22:31
iza: tak widze ale do D to czesc wspolna wiec czemy dajemy 0,+∞
9 lis 22:32
Piotr:
dobra to jeszcze rozwiaze 3 warunek :
log(x+1) ≠ 0
log(x+1) ≠ log1
x+1 ≠ 1
x≠0
9 lis 22:33
Piotr:
narysuje Ci
9 lis 22:34
iza:
9 lis 22:37
Piotr:
ojj nie chce sie zaladowac rysunek
narysuj os i zaznacz −1 oraz 0. oba "leca w prawo". widzisz czesc wspolna ?
9 lis 22:37
iza: dzieki bardzo
9 lis 22:37
Piotr:
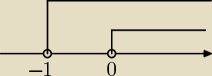
9 lis 22:39
iza: no od−1 do 0
9 lis 22:39
Piotr:
dokonczmy juz to
9 lis 22:40
Piotr:
nieee. tam gdzie oba sie nakladaja.
9 lis 22:41
iza: −1,+∞
9 lis 22:42
Piotr:
nie. od 0 do nieskoczonosci.
9 lis 22:43
iza: nie rozumiem
(
9 lis 22:44
iza: x >0 czyli pomijamy ze x> −1 bierzemy ta wieksza liczbe i od tej liczby zaczymany dziedzine?
tak:((
9 lis 22:49
Piotr:
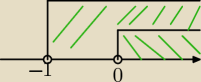
tam gdzie zielone kreski sie spotykaja to masz czesc wspolna.
9 lis 22:49
iza: jej ale kochany jestes teraz widze
9 lis 22:53
Piotr:
teraz rownanie...
9 lis 22:54
iza: logx=−(log(x+1))
x=−x−1
9 lis 23:00
Piotr:
niestety nie.
logx = −log(x+1)
logx = log(x+1)−1
9 lis 23:02
Piotr:
musisz otrzymac log (cos tam) = log (cos tam)
9 lis 23:03
Ajtek:
Co sie tak zaczeriweniłeś
Piotr
Bry
Piotrze .
9 lis 23:04
Piotr:
no nieśmiały jestem
Dobry wieczór
Ajtek
9 lis 23:06
Ajtek:
Nieśmiały
Do 2+2=4 też tak podchodzisz
9 lis 23:07
iza: dlaczego nie moge opuścić log?
9 lis 23:08
iza: daj mu spokój i nie przeszkadzaj Ajtek bo mam we wt kolosa:((
9 lis 23:09
Ajtek:
NIe możesz mieć żadnych liczb/znaków przed logarytmem aby je opuścić.
Zobacz wpis Piotra z godz. 23:03
9 lis 23:09
Ajtek:
iza wpadam z pomocą
.
9 lis 23:10
Piotr:
bo tak jest i juz. zapamietaj to. czyli mamy
x(x+1) = 1
x
2 +x −1 = 0
Δ itd.
9 lis 23:11
iza: to pomoz bo ja si zastrzelę
9 lis 23:11
Piotr:
Δ i pierwiastki umiesz liczyc ?
9 lis 23:13
Ajtek:
Nie strzelaj, tylko zacznij myśleć
. A jak myślenie już nie przychodzi to połóż się spać.
Jutro również jest dzień. Wypoczęta więcej zrozumiesz, niż zmęczona z dobrymi chęciami.
9 lis 23:13
iza: tak umiem,
moze masz racje
9 lis 23:17
iza: ale ze spaniem tez ciezko bo akurat nade mna jest impreza
9 lis 23:18
Piotr:
proponuje bys to dokonczyla. wystarczy polczyc Δ i pierwiastki i sprawdzic czy naleza do
dziedziny. nie wiem czy jutro to bedziesz pamietac. ale jak chcesz.
9 lis 23:19
9 lis 23:22
Piotr:
Δ = 5
| | −1−√5 | |
x1 = |
| nie nalezy do dziedziny |
| | 2 | |
| | −1+√5 | |
x2 = |
| nalezy do dziedziny i jest rozwiazaniem |
| | 2 | |
nie lubie niedokonczonych zadan.
9 lis 23:24
Ajtek:
Jeżeli będę jutro to pomogę. Wieczorem na 100% mnie nie będzie, dokładniej mówiąc po 16−stej
mnie nie bęzie.
9 lis 23:25
iza: hura wyszlo mi tyle samo
9 lis 23:25
Piotr:
Ajtek idzie na radke
ktos na pewno sie znajdzie jutro
9 lis 23:26
iza: ale Ty wyjatkowo cierpliwy jestes
9 lis 23:29
Piotr:
znam bardziej cierpliwych
9 lis 23:31
iza: jejku to nie wiem jak oni to robia
9 lis 23:32
9 lis 23:34
Piotr:
naprawde nie wiem. pewnie tak ale w jakich godzinach to nie wiem.
9 lis 23:36
iza: oki
a napisz mi tylko jeszcze czy log
3(x+1)+log
3(x−1)=1
x=
√2
z:x+1>0
x−1>0
D:x∊(1,+
∞)
9 lis 23:39
Piotr:
dziedzina ok.
rozwiazanie nie.
9 lis 23:42
iza: kurcze
(x+1)(x−1)=1
x
2−1=1
x
2−1−1=0
x
2−2=0
x
2=2
x=
√2
9 lis 23:48
Piotr:
ejj pisalem ze musisz miec musisz otrzymac log (cos tam) = log (cos tam)
czyli 1 zamien na log o podstawie 3.
9 lis 23:51
iza: tak to zrobilam gdzie ten bląd:(
(x+1)(x−1)=1
x2−1=1
x2=1+1
x=√2
9 lis 23:51
iza: to zeby opuścić log musze po znaku = miec tez log
?
9 lis 23:53
Piotr:
a poza tym x2 = 2 ma dwa rozwiazania. jeszcze −√2
9 lis 23:53
Piotr:
tak. po lewej i prawej log
9 lis 23:54
iza: czyli x=2?
9 lis 23:54
iza: czemu?
9 lis 23:55
Piotr:
tak.
wychodzi tez −2 ale odrzucamy bo nie nalezy do dziedziny.
9 lis 23:55
iza: jak wychodzi? mnie nie wyszlo
9 lis 23:56
Piotr:
wyszlo Ci teraz x2 −4 = 0 prawda ?
to (x−2)(x+2) = 0
x=2 lub x = −2
9 lis 23:56
iza: tak, czyli tak powinnam napisac i odrzucic −2?
9 lis 23:58
Piotr:
dokladnie.
pamietaj ze rownanie kwadratowe ma 0,1 lub 2 rozwiazania.
gdy masz x2 − liczba(różna od 0) = 0 to sa dwa rozwiazania
10 lis 00:00
iza: dzieki wielkie ze mi pomagasz .
10 lis 00:02
Piotr:
spoko
10 lis 00:03
Piotr:
200 juz przekroczona
10 lis 00:04
iza: nie wiem jak zrobic x1/3=−4
10 lis 00:07
iza: a nawet nie tak tylko 1/3x=−4
10 lis 00:08
Piotr:
a teraz : 3√x = −4 ?
10 lis 00:10
Piotr:
to drugie brak rozwiazania.
10 lis 00:11
iza: tak wiem ale troche szukalam czegos innego i pokrecilo mi sie
oblicze jeszcze jedno spr mi i
ide spac bo juz glowa mnie boli:((
10 lis 00:12
10 lis 00:15
10 lis 00:16
Eta:
10 lis 00:17
Piotr:
@
iza
to masz na studiach
10 lis 00:17
Eta:
222
10 lis 00:18
iza: tak
10 lis 00:19
Piotr:
o jaa, myslalem, ze liceum
no rekordu to na pewni nie bedzie
10 lis 00:21
iza: log1/3(x+10)+log1/3(7−2x)=−4
Z: x+10>0
x>−10
7−2x>0
x<7/2
D:x∊(−10,7/2)
10 lis 00:25
Piotr:
10 lis 00:29
Eta:
10 lis 00:31
iza: nie wierze
a x
1=−55
x
2=−1
10 lis 00:42
iza: x2∊D
10 lis 00:42
Piotr:
10 lis 00:45
iza: wyjdzie √Δ=9?
10 lis 00:46
Piotr:
tak.
10 lis 00:50
iza: | | 13+9 | | 22 | |
wiec x1= |
| = |
| =−55? |
| | 2*(−2) | | (−4) | |
10 lis 00:53
Piotr:
no jak to mozliwe.
| | 11 | |
skracamy przez 2 i zostaje − |
| co wynosi −5,5 |
| | 2 | |
10 lis 00:54
iza: musimy skracac nie moze zostac tak? a x
2=−1
?
10 lis 00:58
Piotr:
| | 11 | |
mi bardziej odpowiada − |
| ale chcialem pokazac ze sie pomyslilas i ze to rozwiazanie |
| | 2 | |
rowniez nalezy do dziedziny.
x
2 jest ok.
10 lis 01:00
iza: masz racje i przez to zapamietam to napewno
dzieki wielkie jeszcze uciekam juz spac
wykonczyla mnie ta matma
dobranoc i mam nadzieje ze do jutra
10 lis 01:02
Piotr:
do dzisiaj pewnie
dobranoc
10 lis 01:05
