Pomocy!!!!!
Oskar: Dane sa dwa kolejne wierzchołki kwadratu ABCD
A= ( − 1,3)
B= (− 5,1)
Wyznacz współrzędne wierzchołka C.
9 lis 12:19
Artur z miasta Neptuna:
Tylko C?
Masz wierzcholek A oraz B.
Wyznacz wektor AB oraz oblicz dlugosc tego wektora.
Wyznacz wektor prostopadly do wektora AB o takiek samej dlugoscbedzie to twoj wektor BC
majac wektor BC oraz wspoprzedne B jestes w stanie wyznaczyc dwie mozliwe wspolrzedne
wierzcholka C
9 lis 12:23
aniabb:
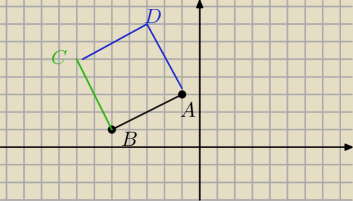
C(−7;5)
prosta AB y=1/2x +3,5
prosta BC y=−2x−9
bok 2
√5
9 lis 12:24
aniabb: fakt..jeszcze na dole C' (−3;−3)
9 lis 12:24
camus: Znajdź prostopadłą do prostej zawierającej AB przechodzącą przez B, po czym ne tej prostej
znajdź punkt oddalny o odległość między A i B.
PS. Będa dwa takie punkty
PS2. Zapisz sobie C jako parę (x,f(x)), będziesz miał wtedy tylko jedną niewiadomą przy |BC|,
f(x) − równanie prostej prostopadłej.
9 lis 12:24
camus: lol, to się nazywa zgranie w czasie
9 lis 12:25
aniabb:
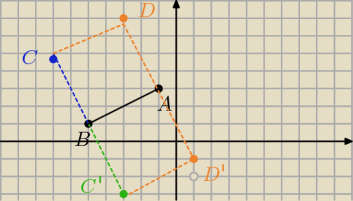
9 lis 12:30
ZKS:
Prosta BC y = −2x − 9
√(−5 − xC)2 + (1 − yC)2 = 2
√5 /
2
(x
C + 5)
2 + (1 + 2x
C + 9)
2 = 20
(x
C + 5)
2 + (2x
C + 10)
2 = 20
| | 1 | |
5x2C + 50xC + 125 = 20 / * |
| |
| | 5 | |
x
2C + 10x
C + 21 = 0 ⇒ x
C = −3 ∨ x
C = −5
9 lis 12:31
aniabb: (−3)*(−5) = 21

> naprawdę tylko żartem

9 lis 12:34
9 lis 12:36
ZKS:
Nie wiem czemu napisałem −5 zamiast −7 chyba zaraz pójdę i dam sobie spokój.

9 lis 12:37
aniabb: nie płapusiaj

..ilość moich literówek powoli bije rekordy

9 lis 12:40
Mila: Jeśli Oskar zna wektory, to pokażę inny sposób.
9 lis 15:37
Tomasz: OK, jeśli mamy wyznaczyć prostą AB:
y =
12 x +
72
i to mam,
później długość boku AB:
|AB| =
√20
i to też mam,
to jak następnie mam wyznaczyć równanie prostej BC?
Skąd mam wiedzieć, że BC:
y = −2x − 9 (podpowiedzi wg klucza)
Później:
| ⎧ | y = −2x − 9 | |
| ⎩ | √(x + 5)2 + (y − 1) = √20 | ,
|
c = (x, y)
Doprowadzenie do układu: x
2 + 10x + 21 = 0
I rozwiązanie: C = (−3, 3) v C = (−7, 5)
3 kwi 02:23
aniabb:
współczynnik kierunkowy prostej BC a= −2 bo
https://matematykaszkolna.pl/strona/42.html więc y= −2x+b
punkt B należy do tej prostej zatem wstawiamy jego współrzędne do wzoru i liczymy b
1= −2*(−5)+b więc b= −9
zatem prosta BC to y= −2x − 9
3 kwi 07:44
 C(−7;5)
prosta AB y=1/2x +3,5
prosta BC y=−2x−9
bok 2√5
C(−7;5)
prosta AB y=1/2x +3,5
prosta BC y=−2x−9
bok 2√5

 > naprawdę tylko żartem
> naprawdę tylko żartem 








 ..ilość moich literówek powoli bije rekordy
..ilość moich literówek powoli bije rekordy 