Przedziały
G: Proszę o pomoc! wyznacz A U B, A ∩ B, A\B oraz B\A jeżeli A=(−1;1),B=<0;2>
5 lis 20:23
5 lis 20:25
G: patrzyłam już pod ten link, chodzi o to ,że nie wiem jak rozwiązać tego typu zadanie jesli
podane mam takie nawiasy. Gdyby oby dwa były otwarte, to nie byłoby problemu. Ale gdy już
pojawiają się domknięte to zaczynam mieć problem.
5 lis 20:27
Mati_gg9225535:
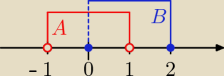
5 lis 20:28
G: czyli to powinno być tak.. ? :
A ∪ B = (−1, 2>
A ∩ B = <O, 1)
A\B = (−1, O>
B\A = (1, 2>
5 lis 20:34
Eta:
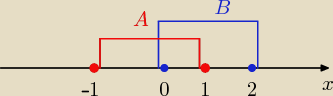
Przedział otwarty ( kółeczka poza przedziałem −−−"uciekły przez otwarte drzwi"
Przedział domknięty ( kółeczka są w przedziale −− "nie mogły uciec, bo drzwi zamknięte"
Zobacz to teraz na rys.
otrzymasz
A\B= (−1,0)
B\A= <1,2>
5 lis 20:43
Eta:
AUB i A∩ B −−− (masz dobrze

5 lis 20:45
G: DZIĘKUJE BARDZO ZA POMOC

))!
5 lis 20:49
Eta:
Podaj teraz A\B i B\ A jeżeli A= <−3, 4> , B= (−1, 7>
zobaczymy, czy zrozumiałeś/aś ,to co ci podałam

5 lis 20:50
Eta:
@
G
Ja czekam

5 lis 21:06
GG: Witaj Eta, bardzo dziękuję ci za pomoc.
A= <−3, 4> , B= (−1, 7>
Wyszło mi:
AUB= <−3,7>
A∩B= (−1,4>
A\B= <−3,−1)
B/A= (4,7>
5 lis 21:10
Gustlik:
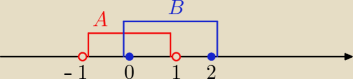 Eta
Eta, bardzo dobre

Z tymi drzwiami super

! Niemniej trzymałbym się tego malowania
(lub nie malowania) kółeczek − dla zmyły, żeby się nauczyciel nie przyczepił, jak zobaczy inny
sposób. Ja jednego ucznia nauczyłem robić bez malowania, tak jak robi
Bogdan, to mu
nauczycielka tego nie uznała. Dlatego robię po nowemu, ale dla zmyły zamalowuje kółeczka, gdy
przedział domknięty.
Dodam, że ja też stosuję takie obrazowe tłumaczenia nawiązując do sytuacji wziętych z życia.
Oto przykłady:
− mnożenie sum algebraicznych czyli "nawiasów": (a+b)(c+d)
a+b to rodzina Nowaków, c+d − to rodzina Kowalskich. Obie rodziny spotykają się na grillu i
każdy z Nowaków się wita z każdym z Kowalskich,
− przenoszenie wyrażeń w równaniach i nierównościach z lewej strony na prawą i odwrotnie:
LEWICA = PRAWICA jak polityk z lewicy przejdzie do prawicy to zmienia logo, czyli znak,
odwrotnie również, zmiana loga to zmiana znaku,
− suma zbiorów: AUB A − majątek Antka, B − majątek Basi, Antek żeni się z Basią i dotychczasowy
majątek kazdego z nich staje się wspólny, oboje korzystają z całości (pomijam tutaj kwestie
prawne),
− część wspólna zbiorów A∩B − to, co Antek i Basia kupili za wspólną kasę przed ślubem,
− różnica zbiorów A\B − na pudełkach − z pudełka A wyjmujemy mniejsze pudełko B − zostają
tylko te rzeczy, które były w pudełku A ale poza pudełkiem B, odwrotnie tak samo,
− porządkowanie wielomianów − jak z wchodzeniem do tramwaju czy autobusu (zgodnie z zasadami
kultury oczywiście) − starsi mają pierwszenstwo, a potem idą młodsi, tutaj starsi to "x"−y z
wyższymi potęgami,
Takie tłumaczenie dużo daje, zwłaszcza uczniom słabszym. Ostatnio jeden z nich zapytał mnie,
dlaczego sumując przedziały AUB nieraz powstaje jeden większy przedział, a nieraz trzeba pisać
jako sumę dwóch osobnych. Wytłumaczyłem mu to tak: tak sie składa, że mam pół domku (tzw.
bliźniaka) i mówię chłopakowi: wyobraź sobie, ze kupuję drugą połowę domku od sąsiadki i co
robię? Przebijam drzwi w ścianie, żeby mieć przejście do tamtej części i rozbieram płot, żeby
połączyć podwórka i robię jedną całość z nieruchomości. To tak, jak ze "stykającymi" się
przedziałami − można je połączyć w całość. A ten drugi przypadek − kupuję dom od sąsiadki
mieszkającej naprzeciwko − i co? Nie mogę połączyć ani budynków, ani podwórek, bo nie dość że
są osobne, to jeszcze przedzielone ulicą. Mam więc dom A w sumie z domem B, ale są to nadal
dwie osobne nieruchomości.
5 lis 23:21
kasia: ŚWIETNE

!
6 lis 12:01

 Przedział otwarty ( kółeczka poza przedziałem −−−"uciekły przez otwarte drzwi"
Przedział domknięty ( kółeczka są w przedziale −− "nie mogły uciec, bo drzwi zamknięte"
Zobacz to teraz na rys.
otrzymasz
A\B= (−1,0)
B\A= <1,2>
Przedział otwarty ( kółeczka poza przedziałem −−−"uciekły przez otwarte drzwi"
Przedział domknięty ( kółeczka są w przedziale −− "nie mogły uciec, bo drzwi zamknięte"
Zobacz to teraz na rys.
otrzymasz
A\B= (−1,0)
B\A= <1,2>

 ))!
))!


 Eta, bardzo dobre
Eta, bardzo dobre  Z tymi drzwiami super
Z tymi drzwiami super  ! Niemniej trzymałbym się tego malowania
(lub nie malowania) kółeczek − dla zmyły, żeby się nauczyciel nie przyczepił, jak zobaczy inny
sposób. Ja jednego ucznia nauczyłem robić bez malowania, tak jak robi Bogdan, to mu
nauczycielka tego nie uznała. Dlatego robię po nowemu, ale dla zmyły zamalowuje kółeczka, gdy
przedział domknięty.
Dodam, że ja też stosuję takie obrazowe tłumaczenia nawiązując do sytuacji wziętych z życia.
Oto przykłady:
− mnożenie sum algebraicznych czyli "nawiasów": (a+b)(c+d)
a+b to rodzina Nowaków, c+d − to rodzina Kowalskich. Obie rodziny spotykają się na grillu i
każdy z Nowaków się wita z każdym z Kowalskich,
− przenoszenie wyrażeń w równaniach i nierównościach z lewej strony na prawą i odwrotnie:
LEWICA = PRAWICA jak polityk z lewicy przejdzie do prawicy to zmienia logo, czyli znak,
odwrotnie również, zmiana loga to zmiana znaku,
− suma zbiorów: AUB A − majątek Antka, B − majątek Basi, Antek żeni się z Basią i dotychczasowy
majątek kazdego z nich staje się wspólny, oboje korzystają z całości (pomijam tutaj kwestie
prawne),
− część wspólna zbiorów A∩B − to, co Antek i Basia kupili za wspólną kasę przed ślubem,
− różnica zbiorów A\B − na pudełkach − z pudełka A wyjmujemy mniejsze pudełko B − zostają
tylko te rzeczy, które były w pudełku A ale poza pudełkiem B, odwrotnie tak samo,
− porządkowanie wielomianów − jak z wchodzeniem do tramwaju czy autobusu (zgodnie z zasadami
kultury oczywiście) − starsi mają pierwszenstwo, a potem idą młodsi, tutaj starsi to "x"−y z
wyższymi potęgami,
Takie tłumaczenie dużo daje, zwłaszcza uczniom słabszym. Ostatnio jeden z nich zapytał mnie,
dlaczego sumując przedziały AUB nieraz powstaje jeden większy przedział, a nieraz trzeba pisać
jako sumę dwóch osobnych. Wytłumaczyłem mu to tak: tak sie składa, że mam pół domku (tzw.
bliźniaka) i mówię chłopakowi: wyobraź sobie, ze kupuję drugą połowę domku od sąsiadki i co
robię? Przebijam drzwi w ścianie, żeby mieć przejście do tamtej części i rozbieram płot, żeby
połączyć podwórka i robię jedną całość z nieruchomości. To tak, jak ze "stykającymi" się
przedziałami − można je połączyć w całość. A ten drugi przypadek − kupuję dom od sąsiadki
mieszkającej naprzeciwko − i co? Nie mogę połączyć ani budynków, ani podwórek, bo nie dość że
są osobne, to jeszcze przedzielone ulicą. Mam więc dom A w sumie z domem B, ale są to nadal
dwie osobne nieruchomości.
! Niemniej trzymałbym się tego malowania
(lub nie malowania) kółeczek − dla zmyły, żeby się nauczyciel nie przyczepił, jak zobaczy inny
sposób. Ja jednego ucznia nauczyłem robić bez malowania, tak jak robi Bogdan, to mu
nauczycielka tego nie uznała. Dlatego robię po nowemu, ale dla zmyły zamalowuje kółeczka, gdy
przedział domknięty.
Dodam, że ja też stosuję takie obrazowe tłumaczenia nawiązując do sytuacji wziętych z życia.
Oto przykłady:
− mnożenie sum algebraicznych czyli "nawiasów": (a+b)(c+d)
a+b to rodzina Nowaków, c+d − to rodzina Kowalskich. Obie rodziny spotykają się na grillu i
każdy z Nowaków się wita z każdym z Kowalskich,
− przenoszenie wyrażeń w równaniach i nierównościach z lewej strony na prawą i odwrotnie:
LEWICA = PRAWICA jak polityk z lewicy przejdzie do prawicy to zmienia logo, czyli znak,
odwrotnie również, zmiana loga to zmiana znaku,
− suma zbiorów: AUB A − majątek Antka, B − majątek Basi, Antek żeni się z Basią i dotychczasowy
majątek kazdego z nich staje się wspólny, oboje korzystają z całości (pomijam tutaj kwestie
prawne),
− część wspólna zbiorów A∩B − to, co Antek i Basia kupili za wspólną kasę przed ślubem,
− różnica zbiorów A\B − na pudełkach − z pudełka A wyjmujemy mniejsze pudełko B − zostają
tylko te rzeczy, które były w pudełku A ale poza pudełkiem B, odwrotnie tak samo,
− porządkowanie wielomianów − jak z wchodzeniem do tramwaju czy autobusu (zgodnie z zasadami
kultury oczywiście) − starsi mają pierwszenstwo, a potem idą młodsi, tutaj starsi to "x"−y z
wyższymi potęgami,
Takie tłumaczenie dużo daje, zwłaszcza uczniom słabszym. Ostatnio jeden z nich zapytał mnie,
dlaczego sumując przedziały AUB nieraz powstaje jeden większy przedział, a nieraz trzeba pisać
jako sumę dwóch osobnych. Wytłumaczyłem mu to tak: tak sie składa, że mam pół domku (tzw.
bliźniaka) i mówię chłopakowi: wyobraź sobie, ze kupuję drugą połowę domku od sąsiadki i co
robię? Przebijam drzwi w ścianie, żeby mieć przejście do tamtej części i rozbieram płot, żeby
połączyć podwórka i robię jedną całość z nieruchomości. To tak, jak ze "stykającymi" się
przedziałami − można je połączyć w całość. A ten drugi przypadek − kupuję dom od sąsiadki
mieszkającej naprzeciwko − i co? Nie mogę połączyć ani budynków, ani podwórek, bo nie dość że
są osobne, to jeszcze przedzielone ulicą. Mam więc dom A w sumie z domem B, ale są to nadal
dwie osobne nieruchomości.
 !
!