wart. bezwzgl. Kejt: Moja ulubiona wartość bezwzględna Jeśli x<−2, to wyrażenie |1−|x+1|| jest równe: A. −2+x B. −x C. 2+x D. −2 −x niech mi ktoś tylko proszę powie jak..policzę sama

ZKS: Dla x < −2 wartość x + 1 jest > 0 czy < 0?

Kejt: mniejsza od zera

Mila: x+1≥0 ⇔x≥−1 Dla x∊<−1;∞) |x+1|=x+1 licz dalej, a raczej rozumuj.

Saizou : dal x<−2 lx+1l=−x−1 l1−(−x−1)l=l1+x+1l=l2+xl=−2−x

Kejt: i zepsuł ale dziękuję

Saizou : prosi o wybaczenie

Kejt: ale nie ma czego wybaczać...szarlotki?

Saizou : w celach rehabilitacji:

	5lx+7l−3
Jaką najmniejszą wartość może mieć podane wyrażenie
	2

ZKS:

	3
Jest jakiś haczyk czy to jest −		?
	2

Saizou : witaj ZKS, a jak myślisz

Kejt: −1,5?

ZKS: Witam Saizou. Myślę że ... nie.

Kejt: no tak..było odświeżyć..

ZKS: Dobrze że nie odświeżałaś to sobie zrobiłaś i nie sugerowałaś się.

Saizou : łapcie a Kejt swoje zadanie |1−|x+1||, możesz zrobić graficznie

ZKS: Kejt 159620 zrób to zadanie.

Mila: Zadanie dla Kejt Sporządzić wykres funkcji: y=2^|log_1/2x|

	1
podstawą logarytmu jest
	2

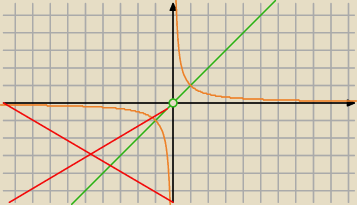
Kejt: (ma być tylko I ćwiartka) tak?