matura xxx: zad.1Okrąg o promieniu 5cm przecięto prostą odległą od środka okręgu o 3cm.Oblicz długość cięciwy,której końcami są punkty przecięcia się się prostej z okręgiem. zad.2napisz równanie prostej przechodzącej przez punkt A=(2,1) i nachylonej do osi x pod kątem 60⁰ zad.3 objętość walca jest równa 72π a jego wysokość ma długość 8.Oblicz obwód l podstawy tego walca nie wiem jak zrobić te zadania pomoże ktoś? próbowałam już chyba milion sposobów i nic

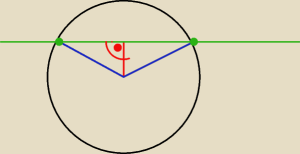
♊: @ zad 1 Niebieskie odcinki to promienie okręgu Czerwony odcinek to odleglość prostej od środka okręgu (odległosc punktu d prowtej mierzymy pod kątem prostym) Zielona prosta to ta prosta. Powstał trójkąt równoramienny − poradzisz sobie dalej ?

Edek: Zad.1 powstaje ma trójkąt prostokątny 3²+c²=5² c=4 Zad.2 y=ax+b 1=2a+b b=1−2a y=ax+1−2a tgα=60⁰=√3 a=tgα a=√3 y=√3x+1−2√3 Zad.3 V=πr²h 72π=πr²h 72=r²h r²=9 r=3 Obw=2πr=6π

♊: @ zad 2 Kąt nachylenia prostej do prostej masz tutaj opisany: 1212 Powinnaś dać sobię radę ;). @ zad 3 Jaki jest wzór na objętość walca? Co możesz z niej uzyskać ? Jak z pola koła można obliczyć obwód ?

xxx: dziękuje