Analityczna :( PuRXUTM: Oblicz miarę kąta między stycznymi do okręgu x²+y²+2x−2y−3=0 poprowadzonymi przez punkt A=(2,0). Przekształciłem równanie okręgu do postaci (x+1)²+(y−1)²=5

	1
Obliczyłem że te proste mają wzór pr. k: y=−2x+4 pr. l: y=		x−1
	2

Jak teraz obliczyć ten kąt ? wiem że a=tgα dla pr.k −2=tgα

	1
dla pr.l		=tgβ tylko co dalej bo to chyba α i β nie wychodzą dokładne
	2

Ajtek: 1228 może to coś pomoże.

Ajtek: I zerknij tutaj 163642 .

PuRXUTM: Witaj Ajtku , szkoda tylko że takiego wzory w szkole nie mieliśmy Kurde, ale spaściłem dzisiaj podstawę z analitycznej 2 zadania źle ehhh.

Ajtek: Cześć PuRXUTM . Spokojnie, nie myli się ten co nic nie robi

AC: Nie sprawdzałem czy dobrze obliczyłeś ale jeśli tak to widać że kąt jest 90^o

	1
bo współ. spełniaja relacje k1= −
	k2

PuRXUTM:

PuRXUTM: AC − o kurde ale ze mnie nieogar, nie wiem co się ze mną dzieje. Mógłbyś to AC sprawdzić ?

Piotr: http://www.wolframalpha.com/input/?i=plot%20x%5E2%2By%5E2%2B2x-2y-3%3D0%2C%20y%3D-2x%2B4%2C%20y%3D(1%2F2)x-1&t=crmtb01

AC: Wow wyliczyłem wychodzi że k₁=−2 k₂=1/2

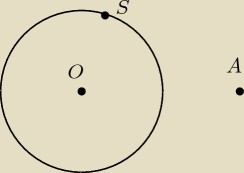
AC: OS=√5 OA=√(2−(−1))²+(0−1)²=√10 Z Pitagorasa SA=√5 czyli trójkat jest prostokatny irównoramieny czyli ∡OAS=45^o z drugą jest identycznie czyli kąt między nimi jest 90^o

PuRXUTM: dzięki