Logarytmy
studentpg93: Jak obliczyć takie coś?:
log
32 x log
43 x ... x log
109
x to znak mnożenia, jakby co
28 paź 22:13
aniabb: zapisać w odwrotnej kolejności i skorzystać że logab*logbc=logac
28 paź 22:15
sushi_gg6397228:
zamien wszystko na podstawe 10
28 paź 22:16
aniabb: wynik log102
28 paź 22:17
aniabb: po co skoro się skraca od razu
28 paź 22:17
studentpg93: a skąd taki wzór
28 paź 22:17
Ajtek:
Hej
aniabb 
.
Tego zworku to nie pamiętam
28 paź 22:17
Ajtek:
Wyprowadzony już, faktycznie działa
.
28 paź 22:21
aniabb: wzór na zmianę podstawy w wersji bezmianownikowej
28 paź 22:23
28 paź 22:24
studentpg93: i mam teraz coś takiego:
log42*log64*log86*log108*
28 paź 22:24
aniabb: drugi raz to samo
28 paź 22:28
studentpg93: a wzór już sprawdziłem i go kumam
28 paź 22:28
studentpg93: No faktycznie! Dzięki wielkie
28 paź 22:29
aniabb: proszę
28 paź 22:31
Mila: | | log2 | |
log32 * log43 *log54* .. ... log98*log109= zamiana logarytmów [log32= |
| }] |
| | log3 | |
| | log2 | | log3 | | log4 | | log8 | | log9 | |
= |
| * |
| * |
| *............... |
| * |
| = |
| | log3 | | log4 | | log5 | | log9 | | log10 | |
28 paź 22:34
Ajtek:
Hej
Mila .
28 paź 22:36
studentpg93: | | 1 | |
Czy mogę liczbę 2 zamienić na log12 |
| |
| | 4 | |
28 paź 22:38
Ajtek:
Sprawdź z definicji logarytmu
.
28 paź 22:40
studentpg93: No i się wszystko zgadza
28 paź 22:42
Ajtek:
To dobrze
.
28 paź 22:43
studentpg93: a mając coś takiego:
3x − 5x > 0
28 paź 22:43
Ajtek:
3x>5x /:5x
Dasz sobie dalej radę?
28 paź 22:45
aniabb: 3
x>5
x
(3/5)
x>(3/5)
0
x<0
28 paź 22:46
aniabb: podstawą ułamek więc zmiana znaku nierówności
28 paź 22:46
Ajtek:
NIe tyle ułamek, co liczba z przedziału (0;1), czyż nie
28 paź 22:47
studentpg93: Okej, dzięki
To jeszcze nie koniec! xd już nie będę nowego wątku zakładał, tylko tutaj będę
pytał
Wy jeszcze nie śpiący?
28 paź 22:50
aniabb: ułamek właściwy
28 paź 22:53
aniabb: jeszcze niee bo czas nam zmienili
28 paź 22:53
Ajtek:
Ułamek właściwy jest ok
28 paź 22:54
studentpg93: okej, to teraz trochę porysuję funkcje logarytmiczne..
28 paź 22:58
Ajtek:
Rysuj, chętnie pooglądam ładne obrazki
.
28 paź 22:58
studentpg93:
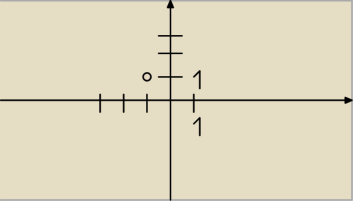
Kurde nie wiem jak mam wam narysować y=−log
2x+1, więc opiszę ją. To kółko otwarte, to miejsce,
gdzie rozpoczyna swój bieg moja funkcja i zbliża się powoli do osi OY, ale jej nie przecina.
Funkcja idzie takim łukiem i jest malejąca.
28 paź 23:13
Ajtek:
Jak wygląda liczba logarytmowana:
(x+1) czy x
28 paź 23:22
studentpg93: x
28 paź 23:23
Ajtek:
Narysuj wykres funkcju y=log
2x
Przesun ją o 1 w górę, a następnie odbij wzgledem osi Ox
28 paź 23:24
studentpg93: hmm.. właśnie zastanawiam się jaka jest kolejność. I czemu względem osi X
a nie odbić jej
wzgledem osi OY ?
28 paź 23:28
studentpg93: no dobra, z tym odbiciem to moj blad ;>
28 paź 23:29
studentpg93: Ale jak to jest z kolejnoscia w przekształcaniu ?
28 paź 23:29
aniabb: najpierw odbić potem przesunąc
28 paź 23:30
Ajtek:
Racja
aniabb
28 paź 23:31
aniabb:
S ox f(x) daje −f(x)
S oy f(x) daje f(−x)
28 paź 23:32
aniabb: więc
logx translacja logx +1 symetria −(logx+1) = −logx−1
logx symetria −logx translacja −logx+1
28 paź 23:33
aniabb: kolejność zależy od tego co chcesz osiągnąc
28 paź 23:34
studentpg93: No! To tutaj zrobiłem dobrze
no pomijając fakt, że źle odbiłem..
a co z funkcją y=xlog
√xx. Dziedzina to x∊(0, +
∞)
28 paź 23:34
Ajtek:
Pewnyś z tą dziedzin?
28 paź 23:35
studentpg93: O ile nie pomyliłem się w dziedzinie ;> ale raczej niee
28 paź 23:35
aniabb: a co ma być?
28 paź 23:35
Ajtek:
Zapewne wykres
.
28 paź 23:36
studentpg93: D: x∊(0, +∞) \ {1} teraz okej? ;>>
28 paź 23:37
aniabb: log√xx=2
28 paź 23:38
Ajtek:
Teraz dziedzina ok.
28 paź 23:38
aniabb: wykres y=2x chyba umiecie
28 paź 23:38
studentpg93: Czyli y=2x ?!
28 paź 23:39
Ajtek:
Nie umiem
.
28 paź 23:39
studentpg93: Jeny.. Dlaczego ja nie zauważam takich rzeczy.. A na sprawdzianie, czy kolokwium nie będzie
zmiłuj...
28 paź 23:40
studentpg93: Dobra, na dziś mam dosyć
Dzięki za pomoc
Dobranoc!
28 paź 23:44
Ajtek:
Spokojnej
.
28 paź 23:44