analityczna PuRXUTM: Wyznacz współrzędne punktu C tak aby trójkąt ABC był trójkątem prostokątnym wpisanym w okrąg o równaniu (x−3)²+(y−5)²=25 gdzie A=(−1,2), B=(7,8). Proszę o pomoc.

PuRXUTM: podbijam

Eta: |AB|= 2r

PuRXUTM: to wiem

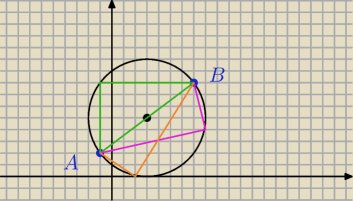
aniabb: C dowolne byle na okregu

PuRXUTM: dalej próbowałem coś kombinować z dł, AB BC AC z prostymi z równaniem okręgu ale i tak dochodziłem do jednego − multum niewiadomych, wiadoma tylko jedna że nie wiem jak to zrobić...

PuRXUTM: no to teraz aniabb mnie zaskoczyłaś

Piotr: przeciez obojetne jaki punkt na okregu !

aniabb: Gdyby AB nie było średnicą to wtedy 2 możliwości.. albo średnicę z A albo średnicę z B

Piotr: https://matematykaszkolna.pl/strona/541.html

aniabb: Ile razy mam Ci powtarzać że w geometrii analitycznej podstawą jest RYSUNEK i to DOKŁADNY

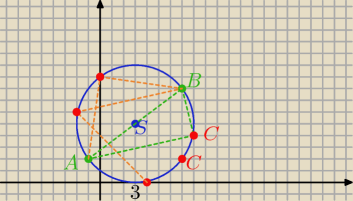
Eta: Takich punktów C jest nieskończenie wiele! Myślę,że czegoś nie dopisałeś w tym zadaniu

aniabb:

PuRXUTM: przepraszam aniabb ale mam takie przekonanie od dawna że rozwiązywanie algebraiczne to najlepsza forma a rysunek jest dla tych co tego nie umieją i że rysunek to zawsze coś nie pewnego, i że się fula punktów nie dostanie bo się zawsze do czegoś nauczyciel przyczepi że tego nie obliczyłeś tylko sobie narysowałeś. Widać będe musiał zmienić przyzwyczajenia

aniabb: mój rysunek to obraz wersji GDYBY AB było cięciwą

aniabb: Po pierwsze teraz każda metoda dobra merytorycznie jest dobra Po drugie dobry rysunek to kontrola Twoich wyników dla Ciebie .. sprawdzasz wszystko na bieżąco

PuRXUTM: Eto − bezpodstawne oskarżenia − tyle jest więcej nie ma. W odpowiedziach jest że C ma dowolne współrzędne należące do okręgu oprócz A i B

PuRXUTM: wiem aniabb wiem muszę po prostu zmienić przyzwyczajenia, zbyt bardzo w LO spodobało mi się rozwiązywanie zadań metodą algebraiczną

aniabb: za moich czasów rysunek służył tylko do sprawdzania..ale i tak całą kombinatorykę zrobiłam metodą obrazkową

PuRXUTM: Kolejne zadanie: Wyznacz współrzędne wierzchołka C trójkąta ABC, jeśli A=(−6,2) i B=(2,−2), a punkt H=(1,2) jest punktem przecięcia wysokości tego trójkąta. mogę wyznaczyć prostą AH przechodzącą przez punkt C ale co dalej ?

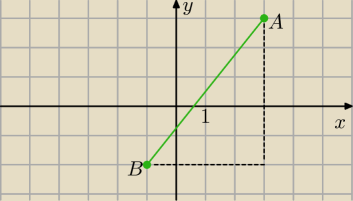
Eta: Geometria analityczna ,to geometria kartezjańska ( rysunek podstawą! Np: zapominasz o wzorze na długość odcinka ( jeżeli punkty A i B są "kratowe" Poczciwy Pitagoras |AB|= √5²+4²= .......

pigor: ... widzę to tak: O=(3,5) − środek okręgu i niech C=(x,y)=?, to (¹₂(x−1)=3 i ¹₂(y+2)=5) lub (¹₂(x+7)=3 i ¹₂(y+8)=5) ⇔ ⇔ (x−1=6 i y+2=10) lub (x+7=6 i y+8=10) ⇔ (x,y)=(7,8) lub (xy)=(−1,2) , więc środek okręgu jest środkiem boku AB −przeciwprostokątnej, zatem C jest wierzchołkiem kata prostego i teraz układ równań np. z iloczynu skalarnego , ale nie koniecznie i . ... to tyle na razie

PuRXUTM: Eto znam ten wzór na dł. odcinka a rozumowania pigora nie pojmuje

Eta: Ja też często go nie pojmuję ( nie jesteś osamotniony

PuRXUTM: pomożesz w tym zadaniu ? Tylko w miarę prostą drogą ?

PuRXUTM: podbijam

Eta: 1/ Wyznacz wsp. kierunkowy prostej AH 2/ Napisz równanie prostej BC , jako prostopadłej do AH i przechodzącej przez B 3/ Wyznacz wsp. kierunkowy prostej AB 4/ Napisz równanie prostej HC jako prostopadłej do AB i przechodzącej przez H Rozwiąż układ równań prostych HC i BC i otrzymasz C

Eta: W tym zadaniu: prosta AH: y=2 to prosta BC: x=2 a dalej już prosto

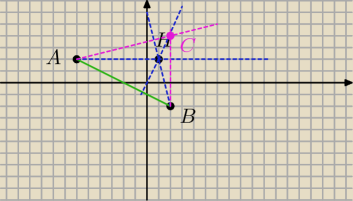
aniabb: C(2;4)

aniabb: oprócz Pitagorasa na długość liczonego z kratek można również współczynniki kierunkowe

PuRXUTM: dzięki