PYTANIE
bartekcmg: Czy prawdą jest, że rozwiązując nierówności, gdy x>0, to rozwiązaniem są 2 przedziały, a gdy
x<0 to rozwiązaniem jest 1 przedział ?
27 paź 10:23
xl:
Bzdury!
27 paź 10:44
bartekcmg: zatem skąd wiadomo kiedy jaki przedział

27 paź 10:46
xl:
To zależy od treści zadania
27 paź 10:50
bartekcmg: na przykład mam do wyznaczenia dziedzinę z czegoś takiego : x(2+x)≥0 jak tutaj określić
dziedzine

27 paź 10:54
xl:
nierówność kwadratowa:
x≤ −2 ⋁ x ≥ 0
27 paź 11:20
Mila:
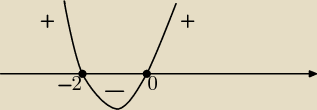 Wartości nieujemne
Wartości nieujemne
x(2+x)≥0 nierówność kwadratowa
x=0 lub x=−2 miejsca zerowe
Rozwiązujemy graficznie; wykresem jest parabola skierowana ramionami do góry.
x(2+x)≥0 dla x≤−2 lub x≥0
Wartości ujemne
x(2+x)<0 dla x∊(−2;0)
27 paź 12:20
bartekcmg: a jeśli mam takie coś: lnx(lnx−3)≥0

z (lnx−3) wyszło mi x≥e
3 a nie wiem co z tym lnx przed nawiasem...
Jaka jest dziedzina tej funkcji

x≥e
3 i ... z lnx≥0 −> x≥e
0 −> x≥1 ... a w
odpowiedziach mam 0<x≤1 − skąd to się bierze?
27 paź 13:19
Mila: lnx*(lnx−3)≥0
D: x>0
lnx≥0 i lnx−3≥0 lub lnx≤0 i lnx−3≤0
x≥1 i x≥e3 lub x∊(0,1> i x∊(0,e3>
x≥e3 lub x∊(0,1>
27 paź 15:23
bartekcmg: Mila, sama napisałaś , że x≥1 , więc skąd x∊(0,1>

o to mi właśnie chodzi, dlaczego ten znak powinien być w drugą stronę i dlaczego

27 paź 17:54
27 paź 17:56
bartekcmg: 
27 paź 17:59
Mila:
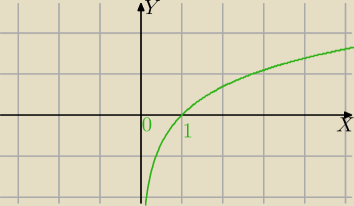
masz dwa warunki:
pierwszy)
lnx≥0 i lnx−3≥0 stąd x≥1 i x≥e
3 część wspólna to x≥e
3
lub
drugi)
lnx≤0 ( zobacz na wykresie kiedy?)i lnx−3≤0⇔
x∊(0;1> i lnx≤lne
3
x∊(0;1> i x≤e
3 część wspólna x∊(0;1>
27 paź 18:00
bartekcmg: . a skąd ten drugi warunek

zawsze myślałem , że wszystko pod pierwiastkiem jest ≥ 0 . Czy
dobrze myślę

27 paź 18:18
Mila: Nie ma tam żadnego pierwiastka.
Jest nierówność:
lnx*(lnx−3)≥0 a nie ln[x(lnx−3)]≥0
27 paź 22:47


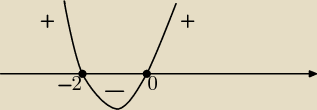 Wartości nieujemne
x(2+x)≥0 nierówność kwadratowa
x=0 lub x=−2 miejsca zerowe
Rozwiązujemy graficznie; wykresem jest parabola skierowana ramionami do góry.
x(2+x)≥0 dla x≤−2 lub x≥0
Wartości ujemne
x(2+x)<0 dla x∊(−2;0)
Wartości nieujemne
x(2+x)≥0 nierówność kwadratowa
x=0 lub x=−2 miejsca zerowe
Rozwiązujemy graficznie; wykresem jest parabola skierowana ramionami do góry.
x(2+x)≥0 dla x≤−2 lub x≥0
Wartości ujemne
x(2+x)<0 dla x∊(−2;0)
 z (lnx−3) wyszło mi x≥e3 a nie wiem co z tym lnx przed nawiasem...
Jaka jest dziedzina tej funkcji
z (lnx−3) wyszło mi x≥e3 a nie wiem co z tym lnx przed nawiasem...
Jaka jest dziedzina tej funkcji  x≥e3 i ... z lnx≥0 −> x≥e0 −> x≥1 ... a w
odpowiedziach mam 0<x≤1 − skąd to się bierze?
x≥e3 i ... z lnx≥0 −> x≥e0 −> x≥1 ... a w
odpowiedziach mam 0<x≤1 − skąd to się bierze?
 o to mi właśnie chodzi, dlaczego ten znak powinien być w drugą stronę i dlaczego
o to mi właśnie chodzi, dlaczego ten znak powinien być w drugą stronę i dlaczego 

 masz dwa warunki:
pierwszy)
lnx≥0 i lnx−3≥0 stąd x≥1 i x≥e3 część wspólna to x≥e3
lub
drugi)
lnx≤0 ( zobacz na wykresie kiedy?)i lnx−3≤0⇔
x∊(0;1> i lnx≤lne3
x∊(0;1> i x≤e3 część wspólna x∊(0;1>
masz dwa warunki:
pierwszy)
lnx≥0 i lnx−3≥0 stąd x≥1 i x≥e3 część wspólna to x≥e3
lub
drugi)
lnx≤0 ( zobacz na wykresie kiedy?)i lnx−3≤0⇔
x∊(0;1> i lnx≤lne3
x∊(0;1> i x≤e3 część wspólna x∊(0;1>
 zawsze myślałem , że wszystko pod pierwiastkiem jest ≥ 0 . Czy
dobrze myślę
zawsze myślałem , że wszystko pod pierwiastkiem jest ≥ 0 . Czy
dobrze myślę