Okręgi. Michał: Dany jest okrąg o ośrodku w punkcie O. Z punktu P, odległego od środka okręgu o 10 cm, poprowadzono dwie proste styczne do tego okręgu w punktach A i B. Oblicz pole trójkąta AOB, jeśli kąt APB = 60 stopni. Prawidłowa odpowiedz to 25√3/4

Mati_gg9225535: https://matematykaszkolna.pl/strona/1249.html https://matematykaszkolna.pl/strona/1468.html wejdz w Zadania+rozwiązania i szukaj podobieństw

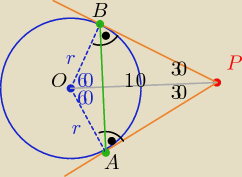
Eta: ΔAPO i BPO są przystające i prostokątne o kątach ostrych 30^o i 60^o to:

	1		1
r=|OB|=		|OP|=		*10= 5
	2		2

ΔOAB jest równoramienny o ramionach r= 5 i kącie między ramionami 120^o ponieważ : sin120^o= sin(180^o−60^o)= sin60^o=..... to:

	1		1
P(ΔABO)=		*r*r*sin120o =		25*sin 60o = ........... dokończ
	2		2