Monotoniczność funkcji szybka pomoc
Kamil: Zbadaj monotoniczność funkcji okresl dziedziny funkcji i zbiory wartości
−y=x2−2x+1
Chodzi mi o to aby udowodnić to za pomoca definicji tylko nie wiem czy jest to mozliwe bez
przedziału Df bo wiadomo że funkcja kwadratowa jest parabola a wiec w pewnym momencie maleje a
w pewnym rosnie
proszę o pomoc jesli ktos wie jak to inaczej zrobic bo wiem że można prosciej liczac
wierzchołek W(p,q) i zbadac czy a>0 a<0 tyle ze jestem na studiach i to raczej byłoby za
proste aby wykazac to w ten sposób
z gory dziekuje za pomoc
16 paź 11:48
aniab: może już miałeś pochodne
16 paź 11:54
Kamil: dopiero wczoraj na wykładzie było cos o tym wspominane ale wątpie żeby akurat w tym przykładzie
to zawrzeć tym bardziej że cwiczenia z tego mielismy tydzien temu
koles podał nam tylko te definicje kiedy rosnie [ (x1≥ x2)⇒f(x1)≥f(x2)) rośnie itd kiedy maleje
parzysta i okresowa
16 paź 11:58
aniab: no to trzeba się pobawić i rozpisać
16 paź 11:59
16 paź 12:00
Kamil: rozpisywaliśmy
założenie −y=x2−2x+1 zamieniam y=−x2−5
Df xeR
x∊Df i −x∊Df
Teza f(x)+f(−x)
dowod
f(x)=−x2−5
f(−x)=−(−x2)−5=−x2−5
f(x)=f(−x)
f jest parzysta w ten sposób czy zrobiłem coś źle ?
16 paź 12:05
Kamil: zaraz nie ten przykład

16 paź 12:06
Kamil: to jest parzystosc
16 paź 12:07
Basia:
−y = x2−2x+1 = (x−1)2
y = −(x−1)2
skoro ma być z definicji to tradycyjnie wyznaczasz wierzchołek W(1;0)
i z definicji dowodzisz, że
x∊(−∞;1> funkcja rośnie
x∊<1;+∞) funkcja maleje
z tego już prawie wynika, że D−1 = (−∞;0>
prawie bo formalnie należałoby pokazać, że limx→±∞f(x) = −∞
więc jeżeli znasz granice to to pokaż
jeżeli już były pochodne, to można inaczej (ale wtedy to nie jest z definicji)
16 paź 12:08
Kamil: df x∊R
f(x1)=−x
12+2x
1−1
f(x2)=−x
22+2x
2−1
−x
12+2x
1−1+x
22−2x
2+1=(−x
12+x
22)2(x
1−x
2) i co dalej

16 paź 12:11
16 paź 12:12
aniab: −(x12−x22)2(x1−x2)=−(x1−x2)(x1+x2)2(x1−x2) ten nawias z minusem z założenia dodatni
ten z plusem zależy od przedziału ..dla ujemnych ujemny więc
−(x1−x2)(x1+x2)2(x1−x2)>0 funkcja rośnie
dla dodatnich dodatni <0 funkcja maleje
16 paź 12:15
aniab: zjadłeś plusa i dlatego zginęło 1

16 paź 12:16
aniab: = −(x1+x2)(x1−x2)+2(x1−x2)=(x1−x2)(x1+x2+2)
i pierwszy nawias z zał. dodatni a drugi sprawdzasz znak ...
16 paź 12:18
Kamil: czyli musze napisac te dwa przypadki bo przedziału określonego nie mam ?
16 paź 12:19
Kamil: chwileczke bo się gubie

to z jakiego przedziału mam brac x
1 i x
2 ?
16 paź 12:21
Kamil: mają byc to liczby Rzeczywiste ?
16 paź 12:25
Basia:
f(x) = −(x2−2x+1) = −(x−1)2
x1 < x2 ≤1 ⇒ x1−1 < x2−1 ≤ 0 ⇒ (x1−1)2 > (x2−1)2 ⇒ −(x1−1)2 < −(x2−1)2 ⇒
x∊(−∞;1> funkcja rośnie
1 ≤ x1 < x2 ⇒ 0 ≤ x1−1 < x2−2 ⇒ (x1−1)2 < (x2−1)2 ⇒ −(x1−1)2 > −(x2−1)2 ⇒
x∊<1;+∞) funkcja maleje
nie zawsze trzeba badać różnicę, czasem można szybciej i prościej
16 paź 12:25
aniab: = −(x1+x2)(x1−x2)+2(x1−x2)= −(x1−x2)(x1+x2 −2)
pierwszy zawsze dodatni sprawdzasz drugi
funkcja rośnie jak x1+x2−2<0 czyli dla x <1
funkcja maleje jak x1+x2−2>0 czyli dla x <1
16 paź 12:28
aniab: ale miał polecenie z definicji
16 paź 12:29
Kamil: własnie mamy takiego postrzelonego wykładowce że nie wiem w koncu czy on chciał to z definicji
cz nie
przed zadaniem tego zadania podal nam własnie te definicje
16 paź 12:33
aniab: to pewnie tak chciał
16 paź 12:37
Basia:
Def:
Funkcja f jest rosnąca w D1 ⇔ ∀x,x1∊D1 [x1<x2 ⇒ f(x1)<f(x2)]
Funkcja f jest malejąca w D2 ⇔ ∀x,x1∊D2 [x1<x2 ⇒ f(x1)>f(x2)]
tyle mówi definicja; badanie różnicy to już wniosek z definicji
w większości przypadków bardzo pomocny, ale akurat z każdą funkcją kwadratową można sobie
poradzić szybciej sprowadzając ją do postaci kanonicznej i używając wyłącznie definicji
16 paź 12:39
Kamil: rozumiem czyli dwa te sposoby co mi pomogłyście są dobre

i dskąd pojawił sie ten zapis x1 <
x2 ≤1 skad ≤1

16 paź 12:44
Kamil: to jest wspołrzedna wierzchołka ?
16 paź 12:46
aniab: tylko zazwyczaj nie chodzi o rozwiązanie tego akurat zadania a o udowodnienie że umiesz
rozwiązywać tego typu zadania więc im bardziej ogólnie tym lepiej ;>
bo jak kazdy większy od 1 to ich suma większa od 2 ..traktujesz je jak różne ale jakby takie
same
16 paź 12:47
Kamil: x1 < x2 ≤1 ⇒ x1−1 < x2−1 ≤ 0 ⇒ (x1−1)2 > (x2−1)2 ⇒ −(x1−1)2 < −(x2−1)2
moze zapytam wprost skąd sie wziął ten zapis, dlaczego wszystko zostalo podniesione do kwadratu
i dlaczego znaki sie odwrociły ?Już czuje że zaczynam was męczyć tym zadaniem ale przez te
trzy miesiące wiekszośc mi się z glowy ulotniła
16 paź 12:50
Basia:
stąd, że z postaci kanonicznej widzę, że inne będzie zachowanie funkcji
dla x∊(−∞;1> a inne dla x∊<1;+∞)
y = −(x−1)2
x−1 ≤ 0 ⇔ x≤1
x−1 ≥ 0 ⇔ x≥1
a kwadrat inaczej działa dla niedodatnich i inaczej dla nieujemnych
dlatego tak
16 paź 12:50
Basia:
a<b≤0 ⇒ a2 > b2
0<a<b ⇒ a2<b2
to już z wiedzy o liczbach po prostu
potem mnożę przez −1
16 paź 12:53
Kamil: dobrze to tak podsumowujac dla tego przykładu jak to powinno wszystko wyglądać
−y=x
3 
16 paź 13:08
Basia:
f(x)= −x
3
tu bym akurat badała sobie różnicę
x
1 < x
2 ⇒ x
1−x
2<0 ⇒
f(x
2) − f(x
1) = −x
23−(−x
13) = x
13 − x
23 = (x
1−x
2)(x
12+x
1*x
2+x
22) < 0
| | x2 | | 3x22 | |
bo x12+x1*x2+x22 = (x1+ |
| )2+ |
| >0 dla dowolnych x1,x2∊R |
| | 2 | | 4 | |
jeżeli chociaż jedno z nich ≠0, a tak być musi skoro x
1<x
2
stąd
f(x
2)<f(x
1) czyli
f(x
1)>f(x
2)
czyli funkcja jest malejąca w R
16 paź 13:28
Kamil: dobrze dziękuje Ci bardzo i Pani która udzielała się wcześniej także dziękuje

Jeszcze mam jedno zadanko a nie chcę zakladac nowego watku
Sprawdź czy jest to funkcja okresowa
y=(x−k)
2 x∊<k−1,k+1> k∊Z df∊r
16 paź 13:40
Basia: teraz już muszę kończyć; może aniab pomoże
tyle, że coś mi tu nie gra
dla np. k=0 mam
y = f(x) = x2 dla x∊<−1;1>
dla k=1 mam
y = f(x) = (x−1)2 dla x∊<0;2>
to jak ta funkcja jest w punkcie x=1 ?
1 należy do oby z tych przedziałów
z (1) f(1) = 1 z (2) f(1) = 0
a to jest niemożliwe, bo sprzeczne z definicją funkcji
albo czegoś nie rozumiem, albo coś tu jest nie tak
16 paź 13:48
Kamil: dobrze w takim razie bardzo Ci dziekuję że mi chociaż troche rozjaśniłaś w głowie pozdrawiam
serdecznie

16 paź 13:53
16 paź 13:57
Kamil: obrazek ciekawy tylko niewiele mi to ułatwia
tu mam definicje na okresowość ∀T że dla każdego x∊Df ((x+T)∊Df i f(x)=f(x+T))
16 paź 14:04
aniab: fakt ona chyba będzie okresowa bo to po prostu poprzesuwane parabolki, ale trudno to nazwać
funkcją ;>
16 paź 14:20
aniab:
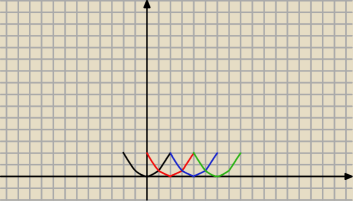
T=1
16 paź 14:26
aniab: (x−k+T)2 =(x−k1)2 ⇔ T∊Z
minT=1
16 paź 14:38
Kamil: to już jest sprawdzenie tak ?
16 paź 14:42
aniab: coś w tym stylu.. nie mam pomysłu na bardziej profesjonalne

16 paź 14:45
Kamil: jakoś w średniej szkole sprawniej mi to szlo a teraz normalnie jakbym dostal zaćmy mózgu
16 paź 14:46
aniab: bo mówią proste rzeczy ale takim językiem że kołkiem staje ;>
16 paź 14:47
Kamil: w sumie to prawda jak siedze na tych wykładach to jak na jakims kazaniu dopiero jak w domu na
spokojnie posiedze pomyslę to zaczynam cos rozumiec tym bardziej że u nas w szkole sredniej
nie przykladano wiekszej wagi do ozanczania symbolami definicji twierdzen posługiwano sie
bardziej przykładami aby to szybko zrozumieć bo na maturze raczej nie ma zadań aby udowodnic
prawo de Morgana
16 paź 14:51
aniab: to norma..ja po olimpiadzie matematycznej w technikum na studiach czułam się tak samo ;>
16 paź 14:53
Kamil: ktory okres jest najgorszy pierwszy semestr czy rok ? u nas bedą robic pewnie przesiew bo za
dużo osób jest
16 paź 14:56
aniab: chyba tylko semestr..potem się człowiek aklimatyzuje ;>
16 paź 14:59
Kamil: dobrze by było to przetrwać

16 paź 15:01



 to z jakiego przedziału mam brac x1 i x2 ?
to z jakiego przedziału mam brac x1 i x2 ?
 i dskąd pojawił sie ten zapis x1 <
x2 ≤1 skad ≤1
i dskąd pojawił sie ten zapis x1 <
x2 ≤1 skad ≤1 

 Jeszcze mam jedno zadanko a nie chcę zakladac nowego watku
Sprawdź czy jest to funkcja okresowa
y=(x−k)2 x∊<k−1,k+1> k∊Z df∊r
Jeszcze mam jedno zadanko a nie chcę zakladac nowego watku
Sprawdź czy jest to funkcja okresowa
y=(x−k)2 x∊<k−1,k+1> k∊Z df∊r

 T=1
T=1

