określ monotoniczność olszyn83: określ monotoniczność

	1
h(x)=		dla (−∞;0)
	x2

	1
f(x)=		dla (1;∞)
	2x + 1

	1
d(x)=x2+		dla <1;∞)
	x2

Artur_z_miasta_Neptuna: krok 1 sprawdzasz dziedzinę funkcji (czy badany przedział w całości mieści się w dziedzinie funkcji) krok 2 obliczasz pochodną funkcji krok 3 określasz w jakich przedziałach pochodna funkcji jest dodatnia/ujemna krok 4 na podstawie kroku 3 określasz monotoniczność funkcji f(x)

tad: ... pierwsze i drugie możesz niezależnie od tego łatwo narysować i poprostu "odczytać" −

olszyn83: jestem na I roku nie bylo jeszcze pochodnych

Artur_z_miasta_Neptuna: olszyn − ale 'coś' było na zajęciach w jaki sposób badacie monotoniczność

Artur_z_miasta_Neptuna: ale jakoś nie chce mi się wierzyć, że ktoś każe określać monotoniczność za pomocą 'tabelki' a nie pochodnych

Artur_z_miasta_Neptuna: chociaż z drugiej strony −−− określenie monotoniczności każdej z tych funkcji nie jest trudna −> wystarczy 'mniej więcej' zrozumieć jak wygląda wykres danej funkcji

olszyn83: cos mi sie wydaje ze dla mnie jest to niewykonalne

aniab: http://www.wolframalpha.com/input/?i=1%2Fx%5E2++from+%E2%88%92%E2%88%9E+to+0++%09++

aniab: monotoniczność bez pochodnych : dla x₂ >x₁ czyli x₂ − x₁ > 0 sprawdzam czy f(x₂) − f(x₁) jest większe ( rosnaca) czy mniejsze ( malejąca) od zera

aniab: czyli

1		1		x12		x22
	−		=		−		=
x22		x12		x12x22		x12x22

	x12 − x22		(x1 − x2)(x1 + x2)
=		=		<0
	x12x22		x12x22

pierwszy nawias z założenia dodatni drugi nawias w badanym przedziale ujemny mianownik dodatni (bo kwadraty ) zatem całość mniejsza od zera a więc funkcja malejąca

olszyn83: o to jest jakis konkret

olszyn83: dzieki

olszyn83: jeszcze taki przykład f(x)=−4x+5 R −4x₂+5−(−4x₁+5)=−4x₂+5+4x₁−5=−4(x₂−x₁)<0 czyli funkcja malejąca zgadza sie?

konrad: w tym przypadku wystarczy odczytać znak 'a', bo jest funkcja liniowa

olszyn83: aniab warajac do przykładu ktory rozwiazałaś (x1 − x2)(x1 + x2) pierwszy nawias nie jest ujemny? x₁<x₂ przeciez

olszyn83: aaa dobrze jest zapomniałem o przedziale

olszyn83: mam takie pytanie w niektórych przykładach jest f(x₁)−f(x₂) a w innych f(x₂)−f(x₁) od czego to zależy

aniab: a no tak ..ujemny więc funkcja rosnąca .. w tych robaczkach tutaj czasem się gubię

aniab: zależy od założeń jakie sobie przyjmiesz ważne aby konsekwentnie

aniab: jeśli x1 >x2 to f(x1) > f(x2) i wtedy rosnąca jeśli x2 >x1 to f(x2) > f(x1) i wtedy rosnąca

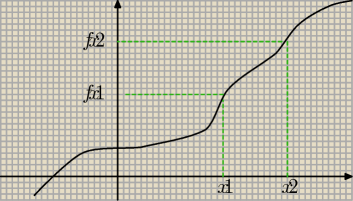
aniab: jak nazwiemy odwrotnie też będzie to samo

olszyn83: ok rozumiem dobrze ze sa jeszcze na tym swiecie ludzie ktorzy wiedza co to jest bezinteresowna pomoc