pomocy pilne !!! MarTa: Czy moze mi ktos wytlumaczyc jaki jest zwiazek miedzy pochodna a monotonicznoscia ? Znam twierdzenia ale musze umiec to wytlumaczyc na przykladzie bo jutro mam egzamin a kompletnie nie wiem jak sie za to zabrac bardzo prosze o pomoc...

Skipper: ...a czym jest pochodna ... (interpretacja geometryczna) ?

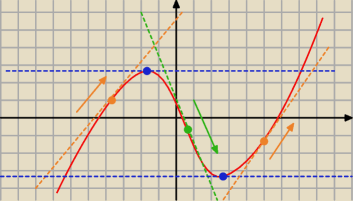
Gustlik: Pochodna funkcji w punkcie jest zawsze równa współczynnikowi kierunkowemu prostej stycznej do wykresu funkcji w tym punkcie. Wiemy, że każdą prostą (z wyjątkiem prostej "pionowej" o równaniu x=c) możemy opisać wzorem funkcji liniowej (równanie kierunkowe) y=ax+b. Proste styczne do wykresu funkcji w punktach, gdzie f(x) jest rosnąca, będą przedstawiały funkcje liniowe także rosnące, a więc o dodatnich współczynnikach kierunkowych (a>0), czyli pochodne w tych punktach będą dodatnie. Analogicznie styczne w punktach, gdzie f(x) jest malejąca będą przedstawiały funkcje liniowe także malejące, a więc o ujemnych współczynnikach kierunkowych (a<0), czyli pochodne w tych punktach wyjdą ujemne. Krótko mówiąc: jaka monotoniczność danej funkcji f(x) w danym punkcie, taka monotoniczność funkcji liniowej o prostej stycznej do wykresu f(x) w tym punkcie. Natomiast tam, gdzie a=0, czyli f'(x)=0, może (ale nie musi !) być ekstremum. Ekstremum będzie, gdy pochodna zmieni znak w tym punkcie. a>0 ⇒ f'(x)>0 ⇒ f(x)↗ a=0 ⇒ f'(x)=0 ⇒ może być ekstremum a<0 ⇒ f'(x)<0 ⇒ f(x)↘ Stąd warunek: tam, gdzie f'(x)>0 to f(x) rosnaca, a tam, gdzie f'(x)<0, to f(x) malejąca.

MarTa: i dlatego wlasnie musimy liczyc pochodna zeby wyznaczyc monotonicznosc?

Gustlik: Tak. Liczysz pochodną, wyznaczasz jej miejsca zerowe (tam mogą być ekstrema), rysujesz przybliżony wykres pochodnej, żeby z wykresu odczytać, gdzie f'(x) jest dodatnia − tam f(x)↗ oraz gdzie f'(x) jest ujemna − tam f(x)↘. W ten sposób wyznaczasz przedziały monotoniczności funkcji.

Gustlik: Tu masz świetnie wytłumaczone przez Jakuba, jak wyznacza się przedziały monotoniczności funkcji: https://matematykaszkolna.pl/strona/385.html .

Gustlik: Jedynie w przypadku prostych funkcji elementarnych, np. liniowa y=ax+b, kwadratowa y=ax²+bx+c,

	ax+b		a
homograficzna y=		lub y=		+q, wykładnicza y=ax i logarytmiczna y=logax
	cx+d		x−p

oraz funkcji powstałych w z prostych przekształceń ich wykresów − przesunięcie o wektor [p, q], symetria, możemy sobie poradzić bez pochodnej − mozna korzystać z typowych własności tych funkcji, a często odczytac ze wzorów, choć pochodną też wyjdzie. Natomiast bez pochodnej ciężko byłoby wyznaczyć monotoniczność np. wielomianów stopnia ≥3 czy funkcji wymiernych bardziej skomplikowanych niż homograficzna, czyli zawierających w ułamku wielomiany stopnia ≥2.

MarTa: dziekuje Ci bardzo bardzo bardzo

Gustlik: