liczby zespolone tomek: Liczby zespolone Jak podać wartości pierwiastków: a) ⁴√1 b) ³√−1 c) ³√i. Gdyby ktoś mógł zrobić jakiś jeden przykład, natomiast ja zrobiłbym resztę − chcę się tego nauczyć.

sushi_gg6397228: z= 1 i liczysz pierwiastki 4 stopnia −−> postac trygonometryczna i x₀, x₁, x₂, x₃

tomek: Nawet tego nie miałem i nie rozumiem do końca zapisu. Mógłbyś coś więcej napisać ?

Krzysiek: https://matematykaszkolna.pl/forum/159136.html http://pl.wikipedia.org/wiki/Wz%C3%B3r_de_Moivre'a ³√−1 z=−1 zamieniam na postać trygonometryczną |−1|=1 φ=π

	π +2kπ		π +2kπ
czyli: 3√−1 =|1|1/3 (cos(		) +isin(		) )
	3		3

k=0,1,2 zatem: dla k=0

	1		√3
z0 =1(cos(π/3) +isin(π/3) )=		+i
	2		2

dla k=1

	π+2π		π+2π
z1 =1(cos		+isin		) =−1
	3		3

dla k=2

	π+4π		π+4π
z2 =1(cos		+isin		)=...
	3		3

sushi_gg6397228: jezeli nie miales, to nie mogli na zajeciach zadac obliczania pierwiastka n−tego stopnia z liczby zespolonej na forum jest duzo zadan o obliczaniu pierwiastka z liczby zespolonej−−> wejsc w wyszukiwarke i znaleść

ZKS: Można też tak. z = ⁴√1 z⁴ = 1 z⁴ − 1 = 0 (z² − 1)(z² + 1) = 0 (z − 1)(z + 1)(z² − i²) = 0 (z − 1)(z + 1)(z − i)(z + i) = 0 ⇒ z = ±1 ∨ z = ±i

tomek: a czemu założyłeś, że φ = π zawsze tak się zakłada?

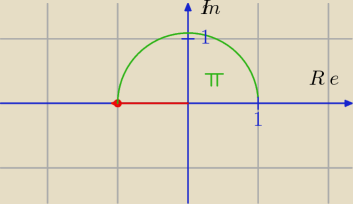
ZKS: Zaznacz sobie punkt A(−1 ; 0) na płaszczyźnie zespolonej i od razu widać jaki to kąt.

tomek: Jak to się zaznacza? Ale zawsze φ = π? I jakbyś mógł napisać określanie kątów czyli: i) sinx > 0 ⋀ cosx > 0

	1		√3
sinα =		⋀ cos =		⇒ α = 30o (x)
	2		2

ii) sinx < 0 ⋀ cosx > 0

	√2		√2
sinα = −		⋀ cosα =		⇒ α = 315o (2π − x)
	2		2

iii) sinx > 0 ⋀ cosx < 0

	√2		√2
sinα =		⋀ cosα = −		⇒ α = 135o (π − x)
	2		2

iiii) sinx < 0 ⋀ cosx < 0 α = (π + x)

ZKS:

tomek: Czyli zawsze będzie φ = 180^o i czy to co wyżej napisałem jest dobrze?

tomek:

ZKS: Jak zawsze φ = 180^o?

	1		√3		π
Przecież dla sin(x) = −		∧ cos(x) =		⇒ x = 2π −		. Więc te wzory:
	2		2		6

sin(x) > 0 ∧ cos(x) > 0 ⇒ to kąt wynosi x sin(x) > 0 ∧ cos(x) < 0 ⇒ to kąt wynosi π − x sin(x) < 0 ∧ cos(x) < 0 ⇒ to kąt wynosi π + x sin(x) < 0 ∧ cos(x) > 0 ⇒ to kąt wynosi 2π − x są dobre.

ZKS: Spróbuj wyznaczyć postać trygonometryczną dla z = 1 − i√3.

tomek: no nie rozumiem dlaczego Krzysiek przyjął, że φ = π. Skąd to wie?

ZKS: Napisałem do jasnej ciasnej żebyś zaznacz na płaszczyźnie zespolonej punkt A(−1 ; 0) bo z = −1 + i * 0 ⇒ z = −1 wtedy zobaczysz skąd ten φ = π. Nawet Ci sam już to narysowałem.

tomek: ok, czyli dla 1 − √3i będzie punkt A(1, √3)?

ZKS: Tego już nie zaznaczaj na płaszczyźnie tylko wyznacz postać trygonometryczną licząc sin(φ) cos(φ) i kąt φ. A poza tym nie podałem 1 + i√3 tylko 1 − i√3 więc punkt inaczej będzie wyglądał.

tomek: z = 1 + i√3 |z| = √1 + 3 = √4 = 2

	1
cosφ =
	2

	√3
sinφ =
	2

zatem φ = 60^o Dobrze ?

tomek: Tak ten kąt wyznaczyć?

ZKS: Napisałem z = 1 − i√3 więc popraw co potrzeba.

tomek: z = 1 − i√3 |z| = √1 + 3 = √4 = 2

	1
cosφ =
	2

	−√3
cosφ =
	2

φ = 300^o ?

tomek:

	√3
tam powinno być: sinφ = −
	2

ZKS: Dobrze.

tomek: a wiesz może jak pokazać, że jeżeli: z = r * (cosφ + isinφ) ⋀ w = t * (cosω + isinω) to wtedy zachodzi: z * w = r * t(cos(φ + ω) + isin(φ + ω)) ?

tomek:

Krzysiek: pomnóż każdy czynnik przez każdy i skorzystaj ze wzorów trygonometrycznych

ZKS: z * w = r * t(cos(φ) + isin(φ))(cos(ω) + isin(ω)) = rt(cos(φ)cos(ω) − sin(φ)sin(ω) + (sin(φ)cos(ω) + sin(ω)cos(φ))i) = rt(cos(φ − ω) + isin(φ + ω)) Korzystałem z cos(x)cos(y) − sin(x)sin(y) = cos(x + y) oraz sin(x)cos(y) + sin(y)cos(x) = sin(x + y)

tomek: L = z * w = (r * (cosφ + isinφ) ) * (t * (cosω + isinω)) = r * t( (cosφ + isinφ) * (cosω + isinω)) = r * t( cosφ * cosω + cosφ * isinω + cosω * isinφ − sinω * sinφ ) = = r * t ( ( cosφ * cosω − sinω * sinφ) + i(cosφ * sinω + cosω * sinφ)) = = r * t (cos(φ + ω) + isin(φ + ω)) = P c.n.d. ?

ZKS: Oczywiście zamiast cos(φ − ω) powinno być cos(φ + ω).

tomek:

	2√2		1
A co jeśli otrzymam takie kąty: cosα =		i sinα =		?
	3		3

tomek: I jeszcze jedno, jak ⁴√1 = z

	1
cosφ =		= 1
	1

sinφ nie istnieje więc φ = 0? Bo szukamy w przedziale <0, 2π)

tomek: I jeszcze jedno, jak ⁴√1 = z

	1
cosφ =		= 1
	1

sinφ nie istnieje więc φ = 0? Bo szukamy w przedziale <0, 2π)

Krzysiek: sinφ=0 zamiast rozpisywać sin i cos łatwo wyznaczyć φ z rysunku φ to jest kąt od dodatniej osi OX do wektora o początku w punkcie (0,0) do punktu (x,y) ,gdzie z=x+yi czyli tu do punktu (1,0) zatem kąt wynosi 0 (wektor pokrywa się z osią OX)

tomek: czyli dobrze napisałem ?

Krzysiek: poza tym: "sinφ nie istnieje" to ok.

tomek:

	2√2		1
A jak będzie cosφ =		i sinφ =		da się kąt wyznaczyć?
	3		3

Krzysiek: jakiś to kąt będzie ale nie wiem ile dokładnie wynosi... może podaj przykład w którym coś takeigo otrzymałeś?

tomek: ok, to dokończę przykład: ⁴√1 z₀ = 1(cos0 + isin0) = 1 ?

	π		π
z1 = 1(cos		+ isin(		) = i
	2		2

z₂ = 1(cosπ + isinπ) = −1

	3π		3π
z3 = 1(cos		+ isin(		) = −i
	2		2

?

tomek: Taki kąt otrzymałem dla 2√2 + i.

Krzysiek: poprzednie zadanie ok co do 2√2 +i wolfram pisze,że: φ≈19,4712 skąd taki przykład? musisz zamienić na postać trygonometryczną?

tomek:

tomek: to chyba ostatni przykład dla upewienia się: ⁴√1 + i = z ⇒ φ = 45^o? zatem:

	45o + 0		45o + 0
z0 = 6√2((cos		) + isin(		)) rozpisywać to dalej czy w takiej
	4		4

formie?

Krzysiek: na początku powinno być: ⁸√2 rozpisz jeszcze z₁ ,z₂ ,z₃

tomek: racja ale reszte tak zostawić?

Krzysiek: ja bym zostawił, możesz też poszukać tabeli z wartościami cos i sin np. dla π/8

tomek:

	405o		405o
z1 = 8√2(cos		+ isin		)
	4		4

	765o		765o
z2 = 8√2(cos		+ isin		)
	4		4

	1125		1125
z3 = 8√2(cos		+ isin		)
	4		4

tomek: a dla ³√2 − 2i ⇒ φ = 315^o

	√2 − √6		√6 + √2
z0 = 6√8 (cos105o + isin105o) =		+		i ?
	4		4

Krzysiek:

	1−√3
cos(105◯ ) =
	2√2

⁶√8 =√2

	1−√3		1−√3
czyli: √2 *		=
	2√2		2

tomek: ok już rozumiem czyli tutaj ⁶√−27 to φ = 180^o

	3		√3
z0 =		+		i
	2		2

z₁ = √3i

	3		√3
z2 = −		+		i
	2		2

	3		√3
z3 = −(		+		i)
	2		2

z₄ = −√3i

	3		√3
z5 =		−		i
	2		2

Tak w ogóle bardzo dziękuję za poświęcony czas

Krzysiek: jak wyniki podniosę do 6 potęgi to wyjdzie −27 więc jest ok.

tomek:

	3
to ostatni przykład: √3 + 4i nawet nie wiem jak początkowy kąt wyznaczyć bo wychodzi
	5

	4
i
	5

Krzysiek: tu nie musisz zamieniać na postać trygonometryczną, żeby to wyliczyć √3+4i =a+bi /² czyli: 3+4i=a² +2abi −b² i teraz rozwiązujesz uklad równan porównując części rzeczywiste i urojone

tomek: Tego nie miałem jeszcze, mógłbyś pomóc?

Krzysiek: 3=a² −b² 4=2ab i rozwiązujesz układ równań wyznaczając a,b

tomek: a czemu nie wyznaczam postaci trygonometrycznej? jak to zauważyłeś?

Krzysiek: Sam zauważyłeś, że nie dasz rady wyznaczyć φ, więc z postacią trygonometryczną nie pójdzie... możesz tez 'trafiać' rozwiązanie co podniesione do kwadratu da: 3+4i np. (2+i)² =4+4i−1=3+4i czasem da się szybko zauważyć rozwiązanie, jednak lepiej je wyliczyć

tomek: ok, dochodzę do momentu gdy b⁴ − 3b² − 4 = 0 t =b² t² − 3t − 4 = 0

	3 − 5
t1 =		= −1
	2

	3 + 5
t2 =		= 2
	2

b = √2 v b = −√2 o to chodziło?

tomek: ok źle: t² − 3t + 4 = 0 i Δ < 0

Krzysiek: http://www.wolframalpha.com/input/?i=%7B3%3Da%5E2+%E2%88%92b%5E2+%2C4%3D2ab+%7D 3=a² −b²

	2
4=2ab ⇒a=
	b

	4
3=		−b2 /*b2
	b2

b⁴ +3b² −4=0

	−3−5
t1 =		=−4
	2

t₂ =1 zatem: b=1 lub b=−1

ZKS: Jest też wzór na obliczenie z = √a + bi

	1
z = ±		(√|z| + a + sgn(b) * i * √|z| − a)
	√2

z = √3 + 4i |z| = √3² + 4² = 5

	1		2√2		√2
z = ±		(√5 + 3 + i√5 − 3 = ±(		+ i		) = ±(2 + i)
	√2		√2		√2