LICZBY ZESPOLONE Godzio: Dla asdf Oblicz: a) ³√i b) ⁵√1 − √3i Rozwiąż równanie: z⁸ = 1 (może bez rozkładania na czynniki )

asdf: z⁸ − 1 = 0 (z⁴ − 1)(z⁴ + 1) = (z² − 1)(z² + 1)(z⁴ + 1) = (z − 1)(z + 1)(z − i)(z + i)(z² − i)(z² + i) = (z − 1)(z + 1)(z − i)(z + i)(z − i)(z + i)( z² + i = 0 z² = −i (x + yi)² = −i x² + 2xyi − y² = −i x² − y² = 0

	−1
2xy = −1 ⇒ y =
	2x

	1
x2 −		= 0
	4x2

4x⁴ − 1 = 0 (2x − 1)(2x + 1) = 0

	1
dla x =		y = −1
	2

	1
dla x = −		y = 1
	2

coś w tym stylu?

Godzio: "Bez rozkładania na czynniki"

Godzio: Przykłady są zastosowaniem postaci trygonometrycznej

aniab: wzór de Moivre'a

Krzysiek: to jeszcze może coś takiego (trudniejsze?) a)³√(2+i)³ b)³√(1+i)⁶

asdf: wzor de moivre'a z⁸ = 1

	pi		pi
z = 1(cos8*1 + isin8*0) = 1(cos8*		+ isin8 *		) = 0
	0		0

tak?

Godzio: https://matematykaszkolna.pl/forum/158979.html Zerknij na przykład, który dałem (z⁶ = 1) i wtedy próbuj, ja muszę uciekać, wieczorem się pomęczymy jak będziesz chciał (koło 21)

asdf: Spoko, dzięki. Wieczorem będę na pewno

asdf: a) ³√i |z| = 1 cosφ = 1 sinφ = 0 φ = 0 ω₀ = (cos0 + isin0) = 1

	2π		2π		1		√3
ω1 = 1(cos		+ isin		) = −		+		i
	3		3		2		2

−1

√3

2π

2π

1

√3

ω2 = (

+

i)(cos

+ isin

) = (−

+

i)2 =

2

2

3

3

2

2

1		√3		3		−1		√3
	+		i −		=		+		i
4		2		4		2		2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	2π		1
cos		= cos120 = −
	3		2

	2π		√3
sin		= cos30 =
	3		2

dobrze?

Krzysiek: zatem φ=π/2 argument najlepiej z rysunku widać (zaznacz sobie punkt (0,1) w układzie, szukany kąt to kąt zawarty między osią (dodatnią) OX a wektorem o początku w (0,0) i końcu (0,1) )

asdf: Rozumiem Krzysku, dzięki. Pomyliły mi się kąty 0^o f. tryg Dzięki

Godzio: I jak z tymi rozwiązaniami (o ile nie śpisz ) ?

asdf: Przygotuje sobie sprawozdanie na laborki z fizyki i skoncze te zadanie. Bedziesz po 23³⁰? Sprawdziłbyś mi i ew. wytknął błędy

Godzio: Pewno będę

asdf: zaraz wrzucę rozwiązanie.

asdf: ⁵√1 − √3i: |z| = 2

	1
cosφ =
	2

	√3		7π
sinφ =−		.........IV ćw........φ =
	2		3

	7π		7π
ω0 = 5√2(cos		+ isin		)
	15		15

prawidłowo? Jak tak to zaraz policzę reszte

asdf: śpisz?

ZKS:

	7		π
φ =		π = 2 +
	3		3

Coś nie gra. Naucz się tak skoro jeden kąt jest dodatni to musi być w I lub dla sinusa też w II albo dla cosinusa w IV. Tutaj mamy cosinus + więc I lub IV ćwiartka dla I ćwiartki kąt wynosi

	π		π		5
x =		korzystamy ze wzorów redukcyjnych 2π −		=		π.
	3		3		3

asdf: Tak, właśnie tak odjąłem, ale nie wiem jak mi wyszło 7π/3.... Oczywiście 5π/3

	π
ω0 = 5√2(cos		+ isinπ/3) = 5√2(1/2 + √3/2i)
	3

teraz jest dobrze?

ZKS: Tak jest dobrze.

asdf:

	11π		11π
ω1 = 5√2(cos		+ isin		)
	15		15

	14π		14π
ω2 = 5√2(cos		+ isin		)
	15		15

tez Ci tyle wyszło?

ZKS:

	11
A skąd to		π?
	15

ZKS:

	π		2		π		2
z1 = 5√2(cos(		+		π) + isin(		+		π) =
	3		5		3		5

	11		11
= 5√2(cos(		π) + isin(		π))
	15		15

	11		2		11		2
z2 = 5√2(cos(		π +		π) + isin(		π +		π)) =
	15		5		15		5

	17		17
5√2(cos(		π) + isin(		π))
	15		15

Godzio: Sorry, nieświadomie zasnąłem z laptopem i zapalonym światłem

asdf: Nie ma sprawy Ja dzisiaj znowu te liczby zespolone...ale juz nadrabiam material

Godzio: Jak coś jeszcze 2 zadania To z⁸ = 1 było źle zrobione

asdf: z⁸ =1 z = ⁸√1 i takie coś liczyć?

Mila: Tak, będzie 8 wartości.

asdf: pfff...to proste. Żartowałęm P.S Za 20 minut podam odp

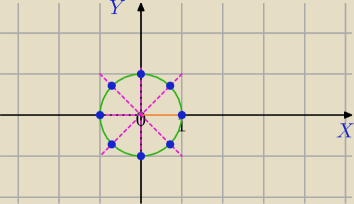
Mila: z₀=1

	2π		2π
z1=cos		+isin		=... itd można odczytać z geometrycznej interpretacji
	8		8

Albo z⁸−1=(z⁴−1)(z⁴+1)=(z²−1)(z²+1)(z⁴+1) z²−1=0 lub z²+1=0 lub z⁴+1=0

asdf: To nie będę już pisać rozwiązania z zeszytu, bo to nie ma sensu. Godzio o jakie dwa zadania Tobie chodzilo?

Godzio: A, w sumie o jedno chodziło(z⁸ = 1), bo nie zauważyłem że oba (to z pierwiastkami) zostały zrobione

asdf: ³√(2 + i)³ = 2 + i? czy to jest inaczej w liczbach zespolonych?

asdf: albo takie coś (podał Krzysiek) ³√(1 + i)⁶ = (1 + i)²?

Godzio: No właśnie, tak nie można Można postawić taką tezę, czy ^kn√z^k = ⁿ√z ?

Godzio: To co napisałeś to jeden z pierwiastków (w obu przypadkach) teraz pytanie jak znaleźć resztę

asdf:

	2π		2π
w1 = w0(cos		+isin		) itd?
	3		3

tylko: z₀ = 2 + i

	2π		2π
z1 = (2 + i)(cos		+ isin		)
	3		3

Godzio: O którym przykładzie mówisz ?

asdf: ³√(2 + i)³

Godzio: I skąd Ci się wziął ten kąt ?

asdf: no tak, zapomnialem o fi, jak tu wyliczyć to?

	1
isin fi =
	4

	1
cos fi =		?
	2

Godzio: No właśnie tutaj tak tego nie wyliczysz, trzeba myśleć inaczej, bo nie mamy fajnego kąta

asdf: z₀ = 2 + i z₁ = √(2 + i)² z₂ = ..? ?

Godzio: Nie mam pomysłu żadnego, jak to prosto wyliczyć

asdf: Czym dokładnie jest pierwiastek z liczby zespolonej? W liczbach rzeczywistych jest to punkt przecięcia się z osią OX, czyli: x² = 1, x = 1 lub x = −1. Dla z² = i, z = i lub z = −i itd...czym one się tak dokładnie różnią? I dlaczego tak jak narysowała Mila są to punkty na okręgu, a nie na kwadracie? Nie miałem tego wszystkiego przedstawionego w formie graficznej tylko tekstowej dlatego mam taki problem chyba z rozwiazaniem tego zadania

Godzio: To raczej się definiuje normalnie, pierwiastek z liczby zespolonej to taka liczba zespolona, w, że wⁿ = z (n − stopień pierwiastka), a zbiór takich pierwiastków to ⁿ√z

asdf: No tak, logicznie definicję rozumiem, ale jak jest takie coś: wⁿ = z 1⁸ = z z₁ = √2

	√2
cos45o =
	1

√2		√2
	=		... czyli coś mi nie pasi
2		1

To już nie rozumiem √2^jakiej da 1? tylko zero, ale każda liczba do zerowej to jeden, czyli coś mi nie pasuje...

Godzio: Tylko, że 1⁸ = 1, bo 1 jest tylko liczbą rzeczywistą. Jeśli już to ⁸√1 = z

asdf: w takim razie z def: ⁸√1 = z ⇒ z⁸ = 1 czyli: z⁸ = 1 w₀ = 1 1⁸ = 1... w₁ = √2 √2⁸ ≠ 1, a tego już nie rozumiem

asdf: z² + 1 = 0, z = −i, z = i z² + 4 = 0, z = −√2, z = √2 Czyli zaznaczamy na osi O_im punkt √2, ale z jaką parą liczb RE?

asdf: oczywiscie: z = −√2 i oraz z = √2i

Godzio: A skąd Ci się bierze w₁ = √2 ? w₀ = 1

	2π		2π
w1 = cos		+ isin
	8		8

Godzio: √2i to para (0,√2i)

asdf:

	pi		pi		√2		√2
w1 = cos		+ isin		=		+		i, czyli punkty
	4		4		2		2

	√2		√2
(		;		) teraz dobrze mysle?
	2		2

Godzio:

	√2		√2
Punkt to (		,		i) − to na płaszczyźnie zespolonej, bo tam zaznaczamy
	2		2

asdf: To w takim razie rysunek Mili jest zły

Godzio: No, tam powinno być Re(z) i Im(z)

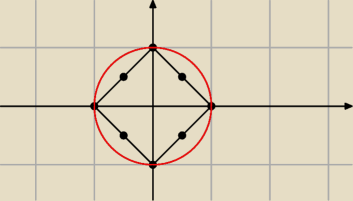
asdf: O to mi chodziło, a jak możesz to przeczytaj post z 18¹¹ i jest tam: I dlaczego tak jak narysowała Mila są to punkty na okręgu, a nie na kwadracie?

Krzysiek: to może rozwiąże zadanie które podałem ³√(2+i)³ mamy pierwiastek 3 stopnia i wiemy,że jedno z rozwiązań to: z=2+i

	2kπ		2kπ
mając jedno rozwiązanie następne łatwo znajdziemy mnożąc przez: (cos		+isin		)
	3		3

gdzie k=0,1,2 ze wzoru de moivre'a :

	φ+2kπ		φ+2kπ
z1/n =|z|(cos		+isin		)
	n		n

	2kπ		2kπ
=(|z| (cosφ +isinφ)(cos		+isin		)
	n		n

gdzie k∊{0,1,...,n−1} |z|(cosφ+isinφ) −jedno z rozwiązań.

asdf: Dzięki Krzysku, ale to chyba nie dla mnie zadanie Znaleźć zbiór liczb rzeczywistych spełniających równanie: x(2 + 3i) + y(5 − 2i) = −8 + 7i 2x + 6i + 5y − 10yi = −8 + 7i 2x − i + 5y − 10yi = −8 ukł. równań: −1 − 10y = 0 2x + 5y = −8 ukł. równań: −1 − 10y = 0 4x + 10y = −16 −−−−−−−−−−−−−−−−−−−−−−− (suma) −1 + 4x = −16 4x = −15

	15
x = −
	4

−15 + 10y = −16 10y = −1

	−1
y =
	10

dobrze?

asdf:

Krzysiek: już drugiej linijki nie rozumiem.. x(2+3i) =2x+3xi ... a Ty napisałeś: 2x+6i podobnie z 'y'

asdf: no tak...co ja zrobilem

asdf: Od tego wszystkiego wszystko się myli x(2 + 3i) + y(5 − 2i) = −8 + 7i 2x + 3xi + 5y − 2yi = −8 + 7i ukł. r.: 2x + 5y = −8

	−7 + 3x
3x − 2y = 7⇒ −2y = 7 − 3x ⇒ 2y = −7 + 3x ⇒ y =
	2

6x + 15y = −24 6x − 4y = 14 11y = −10

	−11
y =
	10

	11
2x −		= −8
	2

2x = −2,5

	5
x = −
	4

prawidłowo teraz jest?

asdf: ?

Krzysiek: źle.. 6x + 15y = −24 6x − 4y = 14 odejmuje stronami czyli: 15y−(−4y) =−24−14 19y=−38 y=−2

asdf: ja nei wiem co jest ze mną dzisiaj

adaś: chyba za długo siedzisz przy matmie

asdf: chyba..dlatego dzisiaj sobie odpuszczam