. asdf: z² = −1 (x + yi)² = −1 x² + 2xyi − y² = −1 x² − y² = −1 2xy = 0 xy = 0 dla: x = 0 ⇒ y = 1 lub y = −1 y = 0 ⇒ x² = −1, czyli odpada pozostaje rozwiązanie: z² = −1 z = −1i lub z = 1i dobrze?

Trivial: z² = −1 ⇔ z = ±i. Nie ma co przekombinowywać.

Godzio: To teraz zadanie * Rozwiąż równanie: z⁴ = 1

Godzio: A żeby rozumieć rozwiązanie, a nie je odwalić, przedstaw to geometrycznie

asdf: a można tak ? z⁴ − 1 = 0 (z² − 1)(z² + 1) = 0 (z − 1)(z + 1)(z² + 1) =0 z = −1 z = 1

Godzio: Myślałem, że to się rozumie samo przez się Rozwiąż równanie w liczbach zespolonych

asdf: geometrycznie? Ja nawet nie wiem jak liczba zespolona wygląda geometrycznie jedynie wiem czym ona jest z tłumaczenia wykładowcy: z = (a,b) = (a,0) + (0,b) = (a,0) + (b,0)(1,0) = a + bi i = (1,0) coś takiego tylko kojarze...

asdf: (x + yi)⁴ = 1 teraz to liczyć ?

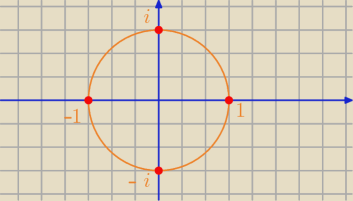
Godzio: Rysowałeś wczoraj Rozwiązania równania z⁴ = 1 znajdują się na okręgu jednostkowym.

Trivial: asdf, wysil się troszkę bardziej. I taka podpowiedź: algebra zespolona działa analogicznie jak rzeczywista.

asdf: Ja to wczoraj rysowałem? Kurde...wczoraj dowiedziałem się czym jest liczba zespolona, a wy już takie zadania tu mi dajecie ledwo potrafię przekształcić z postaci kartezjańskiej na trygonometryczną...Panowie....

Trivial: To zadanko jest bardzo proste. z⁴ = 1 z² = 1 ∨ z² = −1 z = ±1 ∨ z = ±i. I już.

asdf: Dla kogoś, kto w tym siedzi dłużej niż 1 dzień to na pewno

asdf: z² = 1 (x + yi)² = 1 x² + 2xyi − y² = 1 ukł: x² − y² = 0 2xy = 1

	1		1
xy =		→ x =
	2		2y

1
	− y2 = 0
4y2

1 − 4y⁴ = 0 (1 − 2y²)(1 + 2y²) = 0 2y² = −1

	1
y2 = −		<<< brak rozw.
	2

1 − 2y² = 0 −2y² = −1 2y² = 1

	1
y =
	4

	1
dla y =		x = 2
	4

i dalej tędy iść?

Trivial: nie. z² = 1 ma tylko rzeczywiste pierwiastki! (jakie?)

Godzio: z⁴ = 1 ⇔ z⁴ − 1 = 0 ⇔ (z² − 1)(z² + 1) = 0 ⇔ (z − 1)(z + 1)(z² − i²) = 0 ⇔ (z − 1)(z + 1)(z − i)(z + i) = 0 z₁ = 1, z₂ = −1, z₃ = i, z₄ = − i Trzeba kombinować, to akurat było proste zadanko, a rysunek jest, żeby zobaczyć zależność. Jak widać pierwiastki nie są rozłożone przypadkowo. Równanie zⁿ = 1 ma dokładnie n pierwiastków. Dobrze jest to widzieć właśnie na tym rysunku, np. równanie z⁶ = 1 ma pięć pierwiastków, a

	2π		π
każdy jest rozmieszczony co		=		. I do znajdywania tego typu pierwiastków
	6		3

przydaje się np. ostać trygonometryczna. Wówczas od razu mamy rozwiązania: z₁ = 1

	π		π
z2 = cos		+ isin
	3		3

	2π		2π
z3 = cos		+ isin
	3		3

z₄ = − z₁ z₅ = − z₂ z₆ = − z₃ Jak widać przy parzystej ilości pierwiastków, są one rozłożone symetrycznie

Godzio: "z⁶ = 1 ma sześć pierwiastków" oczywiście

Trivial: Godzio, teraz to już trochę chyba przesadzasz.

Godzio: Czemu ? Równanie zⁿ = 1 jest najprostszym, warto na początku od niego wychodzić

Trivial: p. tryg. to chyba za dużo na pierwszy dzień

Godzio: Wczoraj o nią pytał, i nawet pokazywał jak się liczy więc to już pewnie miał machnięte na pierwszym wykładzie

Trivial: aha, to chyba że tak

asdf: Rany boskie...No mialem postac trygonometryczna (wzor Moivre'a). Mam pytanie: jak mam takie coś: z = 1 −i, czyli z = (1,−1), |z| = √2 (1 − i)²⁰ = √20²⁰(cos * 20 * Φ + isin * 20 * Φ) Jak tu obliczyć kąt Φ? Czym on w ogóle jest ?

asdf: No miałem machnięte, babka jakaś opętana jest...na 1 zajęciach...1 wykład i takie rzeczy...

Trivial: asdf, żebyś Ty wiedział co ja miałem czasem na jednym wykładzie... Ale akurat zespolone miałem łagodnie wprowadzane i dobrze przećwiczone.

asdf: Moglibyście mi wytłumaczyć czym się różni Φ od φ? Oraz jak się liczy kąty Φ oraz φ, dla: z = |z|(cosU{1]{2} − isinU{√3{2}}) Tak krok po kroczku, żebym zrozumiał Mam właśnie problem z tym jak się przekształca na kąt φ, reszta puki co bez problemu idzie...

Godzio: sinφ = ...

	π
cosφ = ... ⇒ Φ = 2π −
	4

Trivial: Żeby policzyć (1 − i)²⁰ nie musisz wykorzystywać postaci trygonometrycznej liczby zespolonej. (1−i)²⁰ = ((1−i)²)¹⁰ = (1−2i−1)¹⁰ = (−2i)¹⁰ = 2¹⁰i² = −1024.

asdf: w ogóle to ich wszystkich dobrze po~~....matematyka: trygonometria + liczby zespolone, fizyka: pochodne, macierze, a za tydzien dojdą całki...Na elektronice jakieś tam podstawy do ogarnięcia...na podst. inf. liczenai binarne itd (2h usiąść i chyba ogarne)...ale matma i fizyka to przesada

Trivial: asdf, normalka.

asdf:

	π
Φ = 2π −		, nie bardzo Ciebie rozumiem Godzio
	4

Godzio: Jeżeli masz np:

	√3
sinφ =
	2

	1		π
cosφ = −		To widać, że "kątem podstawowym" jest		, ale coś nie gra bo
	2		3

	1
cosφ = −		, w takim razie nie może być to pierwsza ćwiartka, pytanie gdzie jest sinφ
	2

	π
> 0, a cosφ < 0, jasne jest, że jest to II ćwiartka, no to wystarczy przesunąć		do 2
	3

ćwiartki

√3		π		π		2
	= sin		= sin(π −		) ⇒ φ =		π
2		3		3		3

asdf: kąt φ jest to kąt między |z|, a osią liczb rzeczywistych?

Godzio: Ciężko tak przez forum takie rzeczy się tłumaczy, lepiej by było narysować pokazać co skąd i dlaczego.

asdf: Jest możliwość, żebyś mi to powiedział przez skype + współdzielenie obrazu?

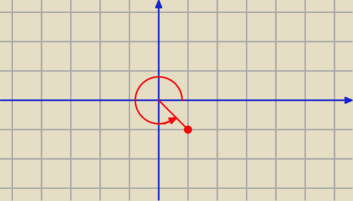
Godzio: To jest ten kąt

	7		π
z = 1 − i ⇒ Φ =		π ( = 2π −		)
	4		4

Godzio: http://www.youtube.com/watch?v=glg1CP2ns2g obejrzyj to, jak nic nie da to przejdziemy do skype

Mila: Wczoraj tłumaczyłyśmy z Basią, poszukaj. Rysowałam z i obliczałam argument.

Mila: Skorzystaj youtube.

asdf: @Mila, poszukam @Godzio Tak się składa, że gdybym mógł używać tych trzech tabelek było by dobrze Ale mam taką babke z matmy, która nie pozwala za bardzo korzystac z takich rzeczy − bo jak twierdzi: tu trzeba

	5
myslec a nie podkladac do wzorów...Każe nawet obliczyć takie coś w pamięci: U{		+
	3

	7
		}{11}...doktorek
	4

Piotr: mam caly kurs etrapez liczby zespolone jak cos

asdf: tez mam jak cos 5,5 gb

asdf: oczywiście kupiłem ..._żartowałem

Piotr: przechodziles ten kurs ?

Godzio: Dlatego tak jak mówię, musisz sobie przesuwać te podstawowe kąty do ćwiartek, które odczytasz ze znaków sinusa i cosinusa: sinx > 0, cosx > 0 −− pierwsza ćwiartka, 0 myślenia, jest to po prostu ten kąt podstawowy, Przykład:

	1		√3		π
sinx =		, cosx =		⇒ Φ =
	2		2		6

sinx < 0, cosx > 0 − IV ćwiartka Przykład

	√2		√2		π
sinx = −		, cosx =		, kąt podstawowy		przesuwamy do IV ćwiartki, tak
	2		2		4

aby wartość sinx i cosx była taka jaką chcemy,

	7
sin(2π − x) i cos(2π − x) zatem Φ = 2π − x =		π
	4

sinx > 0, cosx < 0 − II ćwiartka (patrz przykład wyżej) sinx < 0, cosx < 0 − III ćwiartka

	1		√3		π
sinx = −		, cosx = −		⇒ kąt podstawowy		i przesuwamy do III ćwiartki:
	2		2		6

	7π
sin(x + π), cos(x + π) ⇒ Φ = x + π =
	6

asdf: jeżeli mam takie coś:

	pi
kąt podstawowy =		:
	4

	pi		5pi
ćwiartka: III, czyli to będzie		+ pi =
	4		4

	pi		pi		3pi
ćwiartka: II, czyli to będzie		+		=
	4		2		4

	pi		3pi		7pi
ćwiartka: IV, czyli to będzie		+		=
	4		2		4

?

asdf: @Piotr z liczb zespolonych jestem na 3 zadaniu domowym, dzisiaj moze ogarne do 5 lekcji

Godzio: Tak,

asdf:

	pi
α =
	6

	pi
niech to należy do 3 ćwiartki, każda ćwiartka to		, przyjmijmy, że numer ćwiartki
	2

to niewiadoma = n

	(n − 1)pi		2pi		7π
więc kąt fi to będzie:		+ α, czyli		+ α = π + α =
	2		pi		6

mogę sobie takie coś założyć, żeby łatwiej się to liczyło ?

Godzio: Łojej, jakie skomplikowane wzory, a nie lepiej to zrozumieć i robić "na żywo"

asdf: Nom....postaram się, ale to będzie tez prawidlowe dla IV ćwiartki? kąt fi to kąt między osią liczb rzeczywistych a modułem z?

Godzio: A jak to rozumiesz ? z = 1 − i, |z| = √2, kąt φ to kąt między Re(x), a √2 −− ja nie potrafię tego określić, więc raczej to nie jest to o co pytasz,

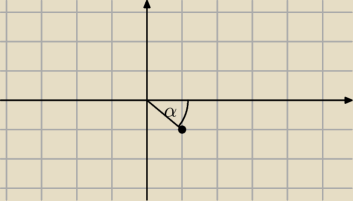
asdf: ja to rozumiem, że |z| to długość wektora od (0,0) do z. A jego wartość = √2 czyli jest to ten kąt? Po co mi sprawdzać w wężyku, kiedy sin to −, plus itd, skoro mogę skorzystać z tego, że punkt z leży w takiej i takiej ćwiartce? Określić wystarczy tylko kąt i starczy?

asdf:

	y
sinΦ =
	|z|

	x
cosΦ =
	|z|

tak?

Godzio: Tak Ale bardziej powiedziałbym, że to kąt między z (bez modułu), a Re

Godzio: Tak

asdf: Ok, dzieki bardzo Ogarniam juz to powoli....a wczoraj nic nie rozumialem, czyli jakis progres jest

Mila: Tak, ale argument φ=360−45=315 Trzeba widzieć interpretację geometryczną i wszystko jest proste.

asdf:

	1
sinΦ =
	2

	−√3
cosΦ =
	2

W jaki sposób przedstawić kąt Φ aby móc skorzystać ze wzorów redukcyjnych? a) Φ = 2pi − alfa b) Φ = pi − alfa c) Φ = pi + Φ d) Φ = alfa Ten punkt to punkt w 4 ćwiartce, czyli to będzie 2pi − alfa?

Godzio:

Ajtek: Witam panowie . Mam wielką prośbę o pomoc w tym wątku 159073. "Uroiłem" sobie, że dam radę, a jednak coś mi nie idzie Z góry dziękuję .

asdf: Witaj Ajtku

asdf: Godzio, Mila i inni którzy udzielili się w tym poście − bardzo dziękuję