liczby zespolone digits: Rozwiazac w dziedzinie zespolonej podane równanie z² + 2iz + (7 − 6i) = 0 proszę o pomoc dopiero co zaczynam ten temat więc nie za bardzo wiem jak to wyliczyć z góry dziękuje

ICSP: umiesz liczyć Δ w trójmianie kwadratowym ?

digits: no tak ale mi nie wychodziło, bo znaki pomyliłem więc już mi wyszło ale mam problem z innym zdaniem. √2+2i to wiem, że 2+2i=a²−b²+2ab później układ równań a²−b²=2 2ab=2 i wychodzi z tego że

	1
b=
	a

a³−1=2a i dalej jakoś nic mi nie wychodzi

ICSP: akurat przykład √2+2i można zrobić ze wzoru de Movier'a ale jak lubisz się bawić √2+2i = a+bi 2 + 2i = a² − b² + 2abi z tego mam że :

	1		1
ab = 1 ⇒ b =		⇒ b2 =
	a		a2

a² − b² = 2

	1
a2 −		= 2
	a2

a⁴ − 2a² − 1 = 0 t = a² , t ≥ 0 t² − 2t − 1 = 0 √Δ = 2√2 t₁ < 0 − sprzeczne

	2 + 2√2
t2 =		= 1 + √2
	2

zatem a₁ = √√2 − 1 oraz a₂ = −√√2 − 1 teraz wystarczy policz b i już zadanie z głowy.

ICSP: i chochlik na końcu Jak zwykle

digits: dzięki ja dopiero zaczynam więc jeszcze nie za dobrze wiem gdzie co i jak stosować ale z czasem myślę, że to ogarne jeszcze raz wielkie dzięki

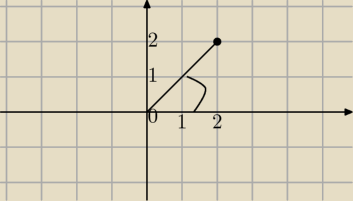
Mila: Skorzystaj z postaci trygonometrycznej liczby zespolonej z=(2+2i) |z|=√8=2√2

	2		√2
sinφ=		=
	2√2		2

	π
φ=
	4

	π   +2*0*π 4		π   +2*0*π 4
z0=√√8(cos		+isin		)=
	2		2

	π		π
=4√8(cos		+isin		)
	8		8

	π   +2*1*π 4		π   +2*1*π 4
z1=√√8(cos		+isin		)=
	2		2

	9π		9π
=4√8(cos		+isin		)
	8		8

digits: mam problem z zadaniem z²+(−1−4i)z+(5+5i)=0 Δ=(−1−4i)²−4(5+5I)=1+8i−16i−20−20i Δ=−19−28i √Δ=√−19−28i √−19−28i=a+bi −19−28i=a²−b²−2ab

	14
2ab=−28 ⇒ a=−
	b

	196
a2−b2=−19 ⇒		−b2=−19 ⇒ b4−19b2−196=0
	b2

b²=u u²−19u−196=0 Δ=361−4*(−196)=361+784=1145 √Δ=√1145 i co dalej z tym zrobić

Mila: https://matematykaszkolna.pl/forum/159360.html