dziedzina funkcji ekonomista: Wyznacz dziedzinę funkcji:

	2√x2−9
a) f(x)=		+x√2−x
	x2+2x−3

	x		7x2
b) f(x)= √		+ln(x−1) +
	2−x		x−3

	3√2−x		ln(1−x)
c)f(x)=		+
	x2−1		2x+6

	ln(x+2)
d) f(x)=		+√9−x2
	ex

	6−3x		2e2x
e) f(x)=√		+
	3−x		ln(x−2)

	1
f) f(x)=√		−1 + ln(x−2x2)
	x2

Mati_gg9225535: https://matematykaszkolna.pl/strona/156.html

Mati_gg9225535: mianownik ≠ 0 i to co pod pierwiastkiem ≥0

ekonomista: a co z pierwiastkami i z logarytmami

Piotr: liczba logarytmowana >0

ekonomista: nie rozumiem, niech ktoś dla przykładu obliczy przynajmniej jeden podpunkt z logarytmem i pierwiastkiem

Mati_gg9225535: b)

	x
D:		≥0 ⋀ x−1>0 ⋀ x−3≠0
	x−2

c) D: x²−1≠0 ⋀ 2x+6≠0 ⋀ 1−x>0 (dla ³√x x∊R)

ekonomista: nie rozumiem tego pierwszego x w b) dlaczego mianowniki są inne

Piotr: @Mati w b) jeszcze 2−x≠0

ekonomista: czy może ktoś mi to wytłumaczyć bo nic nie rozumiem

Mati_gg9225535: Piotr, faktycznie dzieki za uwagę ekonomista, 1) mianownik nie może być równy 0 bo nie dzielimy przez 0 2) pierwiastek kwadratowy istnieje tylko z liczby ≥0 3) w przypadku logarytmu log_ac=b c(liczba logarytmowana) musi być > 0 bo nie może być równe a≠0, a logarytm to przecież potęga a^b=c, gdyby c miało być zerem a musiałoby być zerem lecz w logarytmie po prostu nie może nim być : ) stąd założenie że liczba logarytmowana(c) > 0

ekonomista: i tak nie rozumiem

Mati_gg9225535: mam nadzieje ze tylko 3 przypadku?

ekonomista: a potęgi ?

ekonomista: a dlaczego w b) mianownik jest zmieniony

Piotr: to przeciez literowka

ekonomista: aha, czyli w końcu jak to b) zrobić

Piotr: rozwiazac :

x
	≥ 0 i 2−x≠0 i x−1>0 i x−3≠0
2−x

ekonomista: niech ktoś poda poprawnie

Piotr: a moje nie jest poprawne ?

Mati_gg9225535: kreska ułamkowa to zastępczy znak dzielenia, a w matematyce jest taka reguła jak "cholero nie dziel przez 0!" trzeba się jej trzymać dlatego gdy widzisz niewiadomą x w mianowniku to od razu ten mianownik zapisujesz w postaci (coś tam coś tam) ≠0 pierwiastkowanie to odwrotność potęgowania, pierwiastek parzystego stopnia ⁿ√a=b, gdzie n jest liczbą parzystą (np.2,4,6,...) bⁿ=a, więc to co pod pierwiastkiem nie może być ujemne bo żadna liczba podniesiona do kwadratu lub do potęgi 4,6,8,... (b², b⁴=(b²)²,...)nie jest ujemna:

	2		4
(−1)2=1, 32=9, (−		)2=		,...
	3		9

Mati_gg9225535: czytaj to dopóki nie zrozumiesz

Mati_gg9225535: Piotrze zerknąłbyś na to zadanie 158565 ?

ekonomista: ale b) nie zgadza mi się z kluczem odpowiedzi: x∊(1;2)

Mati_gg9225535: nie szukaj błędu, spróbuj rozwiązać jeszcze raz, sprawdz czy dobrze przepisałeś wszystkie dane

ekonomista: przepisałem, obliczyłem i coś nie tak

ekonomista: niech ktoś to dla przykładu wyliczy

Mati_gg9225535: ja obliczyłem z tych samych założeń i wyszło mi dobrze czy wykonując działania na tym ułamku nie pomnożyłeś obustronnie przez mianownik?

x
	≥0 ⇔ x(x−2)≥0
x−2

ekonomista: nie, zrobiem inaczej

ekonomista: ciekawe jak to niby wyliczyć jak mam x i x²

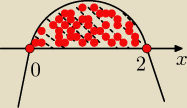
Mati_gg9225535: b)

x
	≥0 ⇔ x(x−2)≥0 ⋀ x−1>0 ⋀ x−3≠0
x−2

D: 2−x≠0 x=0 v x=2 x>1 x≠3 x≠2 (wykres) x∊(1,+∞) x∊ <0,2> ⋀ x∊D x∊ <0,2) w części wspólnej: x∊(1,2)

matema: a mogę prosić o wyliczenie podpunktu a)

Mati_gg9225535: x²+2x−3 ≠ 0 x²−9 ≥ 0 2−x ≥ 0 i bierzesz czesc wspolną

Mati_gg9225535: a odp do a wyglada tak: x ∊ (−∞ , −3)

matema:

	3x2 −1		5		1
mam jeszcze takie zadanie f(x) =		+		+
	x2+1		x2−1		√1

matema: też wyznaczyć dziedzinę i mam z tym problem

Mati_gg9225535: tam jest √1 czy miał być √x ?

matema: przepraszam, √x

Mati_gg9225535: wiec mianownik ≠ 0 i liczba pod pierwiastkiem ≥0 x² + 1 ≠ 0 x² − 1 ≠ 0 √x >0 (gdyby nie był w mianowniku to byłoby √x≥0, ale że mianownik nie może być zerem to √x>0 )

matema: Jak obliczyć; x=√−1 ?

Mati_gg9225535: nie ma czegos takiego, pierwiastek 2 stopnia z liczby ujemnej nie istnieje