Oblicz
m.k: Oblicz:
3√2+√5 + 3√2−√5
7 paź 15:24
7 paź 15:27
m.k: nie ogarniam ;<
7 paź 15:35
Mati:
3√2+√5+3√2−√5 = x/3
(3√2+√5+3√2−√5)3 = x3 podnosisz wg wzoru skróconego mnożenia:
2+√5+ 3(3√2+√52)(3√2−√5) + 3(3√2+√5)(3√2−√52) + 2−√5 = x3 przed
nawias to co sie powtarza w 2 środkowych wyrazach (podkreślonych), √5 się redukuje i
otrzymujesz
4+3[(3√2+√5)(3√2−√5)](3√2+√5+3√2−√5)=x3 zauważasz że na początku
3√2+√5+3√2−√5 oznaczyłeś jako x (na czerwono) więc za 3√2+√5+3√2−√5
podstawiasz x, a z tego pierwszego nawiasu zawsze wyjdzie 1 lub −1 w tym przypadku −1 bo
(3√2+√5)(3√2−√5)= 3√(2+√5)(2−√5)= 3√4−5= −1
więc masz 4−3x=x3
7 paź 16:38
marta: Dzięki!: D
7 paź 16:53
Mati: proszę

7 paź 16:58
Mati: dalej dasz rade prawda?
7 paź 16:58
marta: Mam nadzieję, jak nie to bd pisać : D
7 paź 17:01
Mati: ok

powodzenia
7 paź 17:08
marta: Chyba jednak nie;< ja matmę na podstawię to ogarniam ale nie z rozszerzenia!:<
7 paź 17:11
Mati: no więc masz to równanie:
4−3x=x3
x3+3x−4=0
x3 +3x −4 =0
x3 −x + 4x − 4 = 0
x(x2 −1) + 4(x−1) = 0
x(x−1)(x+1) + 4(x−1) = 0
(x−1)[x(x+1)+4] = 0
(x−1)(x2 +x +4) = 0
x−1=0 ⋁ x2 +x +4 = 0 (liczysz deltę która wychodzi mniejsza od 0 zatem nie ma takiej liczby
spełniającej równanie x2 +x +4 = 0 )
x=1
zatem 3√2+√5 + 3√2−√5} = 1
7 paź 17:22
Mati: to metoda grupowania wyrazów
7 paź 17:23
MATMA: Jesteś wielki! DZIĘKUJĘ TOBIE BARDZO! : D
7 paź 17:26
Mati:
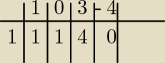
lub tabelką Hornera, bo jeśli W(x)= x
3+3x−4
w(1)=0
(x−1)(x
2 + x + 4) = 0
i jest to samo co wyzej
7 paź 17:28
Mati: w sumie to mały

ale dzieki

7 paź 17:28
MATMA: : D nie bd wnikać już jaki

7 paź 17:51

 powodzenia
powodzenia
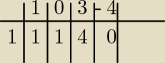 lub tabelką Hornera, bo jeśli W(x)= x3+3x−4
w(1)=0
(x−1)(x2 + x + 4) = 0
i jest to samo co wyzej
lub tabelką Hornera, bo jeśli W(x)= x3+3x−4
w(1)=0
(x−1)(x2 + x + 4) = 0
i jest to samo co wyzej
 ale dzieki
ale dzieki 
