Bardzo proszę o pomoc, bo ja tego wgl nie rozumiem!!! KASIa: Rozwiąż tożsamość: 1) 2cos²α−1= 1−2sin²α 2) sin²(1+cos²α)=1−cos⁴α 3) (2sinα+cosα)²+(sinα−2cosα)²=5

Bogdan: Tożsamości się nie rozwiązuje. Można rozwiązać zadanie z tożsamością. Tu polecenie może być sformułowane np. tak: sprawdź, czy podana równość jest tożsamością. Korzystaj z zależności: sin²α + cos²α = 1, a stąd: sin²α = 1 − cos²α, cos²α = 1 − sin²α Stosuj również wzory skróconego mnożenia.

KASIa: no tak.. a potrafisz to rozwiązać?

Bogdan: Potrafię. Skorzystaj ze wskazówek i spróbuj sama

KASIa: miałam z tego tylko jedną lekcję i rozwiązaliśmy na niej tylko jeden przykład, ja tego nie rozumiem i choćby nie wiem co ja tego nie rozwiąże bo nie umiem.

Aga1.: 1) L=2cos²α−1=2(1−sin²α)−1=2−2sin²α−1=1−2sin²α=P

KASIa: a możesz mi to jakoś wytłumaczyć?

Bogdan: Nie wierzę, że nie potrafisz wstawić 1−sin²x w miejsce cos²x i wykonać mnożenie przez 2

KASIa: ale skąd Ci się wzięło 1−sin²x?

Aga1.: Znasz wzór zwany jedynką trygonometryczną? sin²α+cos²α=1 Z tego wzoru (po przekształceniu) wynika,że cos²α=1−sin²α

KASIa: Ja tego nie rozumiem!

Bogdan:

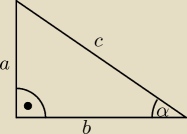
	a		b
W trójkącie prostokątnym:		= sinα,		= cosα
	c		c

Z twierdzenia Pitagorasa:

	a		b
a2 + b2 = c2 /:c2 ⇒ (		)2 + (		)2 = 1 ⇒ sin2α + cos2α = 1
	c		c

a stąd sin²α = 1 − cos²α oraz cos²α = 1 − sin²α

KASIa: no dobrze już troche kapuje to zadanie a te dwa następne?

Bogdan: a² − b² = (a − b)(a + b) a⁴ − b⁴ = (a² − b²)(a² + b²) a⁶ − b⁶ = (a³ − b³)(a³ + b³) itd.

KASIa: dziękuję juz wszystko wiem, dziękuję wszystkim za pomoc

mar and ola:): drodzy przyjaciele proszę pomóżcie mi w tych zadaniach oto link: https://matematykaszkolna.pl/forum/158204.html