Zadania dla mocnych AS: Niech liczy kto chce. Zadanie 1 Napisz taki wielomian o współczynnikach całkowitych, aby jego pierwiastkiem była liczba ³√2 + √5 + ³√2 − √5. Zadanie 2 W trapezie opisanym na okręgu o promieniu r jeden z kątów jest prosty,kąt zaś ostry równa się α. Zbudować ten trapez a następnie obliczyć jego pole.

Godzio: Zad. 1 W(x) = x − 1

AS: Sprytne,ale nie o takie równanie chodziło.

Godzio: A może o takie: x³ + 3x − 4 = 0 ? Mogę też pokazać jak do tego dojść, jeśli to konieczne

Godzio: Naczy wielomian: W(x) = x³ + 3x − 4

Rodney: W zad 2 P=4r² ? Taki wynik mi wyszedl, ale chyba cos zle, bo spodziewalem sie raczej, ze potrzebny bedzie ten kąt α

Rodney: po zastanowieniu sam stwierdzam, ze moje rozwiazanie jest bez sensu, ale sprobuje jeszcze Godzio: jesli moglbys pokazac to chetnie zobacze jak do tego doszedles

Rodney:

	1
co do zad 2 to mam tez propozycje, ze P = r2*(2+		)
	sinα

Teraz dobrze?

Godzio: Rodney najpierw poczekam na odp. ASA Bo jeśli chodzi o jeszcze inny wielomian to nie wymyślę tak szybko

Rodney: No, a nie moglbys pokazac jak doszedles do tego ostatniego? w sumie rozumiem czemu akurat taki jest ale jakos nie moge trafic na odpowiedni tok myslenia zeby dojsc do takiej postaci... jakas wskazowka moze chociaz?

Godzio: Oznacz wyrażenie jako x i podnieś do ³ .... = x /³ I dalej myśl

ZKS:

	1 + √5
2 + √5 = (		)3
	2

Rodney: heh dzieki Godzio Najtrudniejsze w tym bylo to, zeby zauwazyc jak juz otrzymalem x³=4−3(³√2+√81+³√2−√5 to najtrudniej bylo zauwazyc, ze ten nawias przy trojce, ze to jest to co na poczatku uznalismy za x w sumie to na poczatku chcialem tak sprobowac wlasnie poprzez przyrownanie do x, ale jak to rozpisalem to uznalem, ze chyba nic z tego nie bedzie i porzucilem ta droge

Godzio: Najważniejsze, że do tego doszedłeś

Rodney: zajrzalby ktos moze czy moje rozwiazanie jest dobre pod tym zadaniem: https://matematykaszkolna.pl/forum/157303.html ? bo w sumie to szybko kolejne tematy dodaja i spadlo juz dosyc mocno

AS: Odpowiedź Godzia poprawna, o to równanie chodziło. Pole trapezu:

	1
P = 2*r2*(1 +		)
	sinα

Brak w rozwiązaniu konstrukcji trapezu o podanych danych.

Rodney: co do pola to rzeczywiscie pod koniec obliczen zgubilem jedna dwojke i stad ten blad konstrukcja... nie do konca rozumiem polecenie mam zrobic rysunek trapezu, ktory by pasowal do tego zadania?

AS: Nie , mając do dyspozycji odcinek długości r i kąt o rozwartości α, wykreślić tylko przy pomocy ołówka,linijki i cyrkla ten trapez.

Rodney: to w sumie tak podejrzewalem i bylbym chyba w stanie zrobic, ale jak to wykonac w tutejszych warunkach? wrzucic skan czy jak?

AS: Wystarczy podać opis kolejnych czynności.

Rodney: 1) rysuje odcinek |AB|=2r 2) rysuje okregi o srodkach w punktach A i B i promieniu |AB| 3) przez punkty przeciecia okregow prowadze prosta k, ktora dzieli odcinek |AB| na pol w punkcie F 4) rysuje okrag o srodku w punkcie F i promieniu |AF|, zaznaczam punkt G w miejscu przeciecia prostej k i narysowanego okregu 5) z punktu G rysuje okrag o promieniu |FG| 6) z punktu A prowadze odcinek styczny do okregu o srodku G, ale krotszy niz 2r, odcinek konczy sie w punkcie C 7) z punktu C prowadze polprosta m, styczna do okregu o srodku G 8) z punktu B prowadze polprosta n, styczna do okregu o srodku G 9) punkt przeciecie polprostych m i n, oznaczam jako punkt D kat BDC=α promien okregu o srodku G jest rowny r nie wiem czy dobrze, ostatni raz cyrkla uzywalem w gimnazjum, jestem otwarty na krytyke

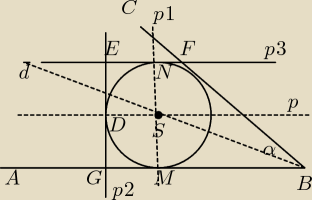
AS: Nie wszystko zrozumiałem z podanego opisu. Dlatego podaję moją propozycję. Zakładam,że znane są konstrukcje wyznaczania kąta , kreślenie prostej równoległej (prostopadłej) do drugiej. 1. Wyznaczam kąt α (<ABC) 2. Wykreślam dwusieczną kąta α (pr. d) 3. Prowadzę prostą równoległą do AB w odległości r. (pr. p) 4. W przecięciu prostych d i p otrzymuję punkt S (środek okręgu) 5. Przez S prowadzę prosta prostopadłą do AB do przecięcia się z okręgiem (punkt N) 6. Przez N prowadzę prostą równoległą do AB (pr.p3) 7. Przez D prowadzę równoległą do MN w odległości r. 8. Czworokąt GBEF jest szukanym trapezem.