Znajdź wszystkie a Rodney: Znalazłem ciekawe zadanie, którego rozwiązania nie znalazłem w internecie, więc może ktoś pomoże Znajdź wszystkie "a" takie, dla których równanie |ax|+x=1 ma dokładnie jedno rozwiązanie. W sumie doszedłem do tego, że a∊<−1;1>, ale nie do końca wiem jak to wykazać. Ktoś pomoże?

...: IaxI=−x+1

...:

asdf: Odpowiedzi to 2 ? Jak się zgadza to podam rozwiązanie

asdf:

Rodney: asdf: odpowiedz to a∊<−1;1>

asdf: to źle mi wyszło

Chicken: DDDD

asdf: Dasz obliczenia?

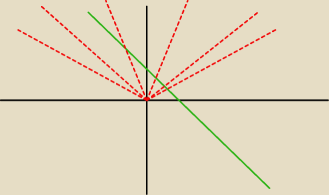
...: na czerwono masz różne przypadki lewej strony na zielono f(x)=−x+1 i popatrz teraz na współczynniki kierunkowe (kiedy jedno rozwiązanie a kiedy dwa) ... wynik masz ok

Rodney: no wlasnie, wpadlem wlasnie na to tylko nie wiem czy takie uzasadnienie mialbym na maturze uznane za poprawne, zaraz napisze obliczenia

Rodney: |ax|+x=1 no to rozbiłem sobie ten nawias na |a|*|x|+x=1 i teraz rozwazam dla x≥0 |a|x+x=1 (|a|+1)x=1 czyli wspolczynnik przy x zawsze bedzie dodatni teraz sprawdzam dla x<0 |a|*(−x)+x=1 (−|a|+1)x=1 sprawdzam wspolczynnik przy x, kiedy bedzie nieujemny −|a|+1≥0 −|a|≥−1 |a|≤1 a∊<−1;1> dobrze rozwiazane? jak by mi to ocenili na maturze?

Godzio: Brakuje trochę eleganckiego komentarza. Napisz to tak jakbyś napisał to na maturze, egzaminator nie wiedziałby dlaczego robisz tak a nie inaczej (co pokazuje 1 przypadek, czego oczekujemy w 2 )

Rodney: no wlasnie nie wiem jeszcze jak bym to napisal na maturze, jestem w 2 klasie i mam dosyc czesto ten problem, ze wiem jak rozwiazac pewne zadanie, ale nie wiem jak je przedstawic w taki wlasnie ladny, przejrzysty, matematyczny sposob

Godzio: No to tak, rozbijanie na przypadki − ok, tyko nie piszesz co z tego wynika Zauważ, że dla x ≥ 0 mamy już jedno rozwiązanie:

	1
x =		nie zależnie od a
	|a| + 1

Zatem dla x < 0 oczekujemy, że takowego rozwiązania nie będzie. x(1 − |a|) = 1, ponieważ x < 0 to rozwiązania nie będzie gdy: 1 − |a| ≥ 0 ⇒ a ∊ <−1,1>