Rozwiąż
Czarek1994:
1) x
3 − 4x
2 + x + 6 = 0
2) (x − 3)(4−x
2)(x+3)
2 ≥ 0
30 wrz 21:55
pigor: 1) ... łatwo zauważyć, że W(−1)=0 , więc grupuję . ...

"pod ten" x= −1 , czyli "pod"
dwumian (x+1) np. tak :
x3−4x2+x+6=0 ⇔ x
3+x
2 −5x
2−5x +6x+6= 0 ⇔ x
2(x+1)−5x(x+1)+6(x+1)= 0 ⇔
⇔ (x+1)(x
2−5x+6)= 0 i np. ze wzorów Viete'a ⇔ (x+1)(x−2)(x−3)= 0 ⇔
x∊{2,−1,3} .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
4)
x ≥1x /* x
2 >0 i
x≠0 ⇒ x
3 ≥x ⇔ x
3−x ≥0 ⇔ x(x
2−1) ≥0 ⇔
⇔ x(x−1)(x+1) ≥ 0 i x≠0 ⇔
x∊<−1;0) U <1;+∞) . ...

30 wrz 22:46
Gustlik: Najlepiej Hornerem, potem delta, a nie kombinacyjnymi metodami typu grupowanie, na maturze nei
ma czasu na takie zabawy:
1 −4 1 6
1 1 −3 −2 4
−1 1 −5 6 0
x=−1 jest pierwiastkiem
(x+1)(x2−5x+6)=0
Δ=1, √Δ=1
x1=2, x2=3
Odp: x=−1 v x=2 v x=3
30 wrz 22:51
Czarek1994: Dzięki rozjaśniłeś mi trochę w mej makówce

30 wrz 22:54
Czarek1994: Tylko że tkz. Hornera nie miałem na lekcji

jeśli mam tak robić to wypadało by coś na ten
temat wiedzieć

30 wrz 22:55
Czarek1994: i wzorów viete'a też nie miałem

30 wrz 22:58
30 wrz 23:00
Czarek1994: Ok zapoznam się z tą lekturą

30 wrz 23:04
krystek: @Gustlik ja przedwojenna Hornera nie znałam i też liczyłam . Horner nie rozwija logicznego
myślenia − moim skromnym zdaniem.
30 wrz 23:04
Czarek1994: A 2 jak zrobić ? jakoś prosto ?
30 wrz 23:07
krystek: (x−3)(2−x)(2+x)(x+3)2≥0
teraz m zerowe Pamiętaj ,że −3 jest pierwiastkiem podwójnym i "wężyk" cyli wykres i masz
30 wrz 23:11
krystek:
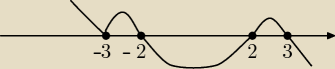
30 wrz 23:13
Czarek1994: "Pamiętaj ,że −3 jest pierwiastkiem podwójnym i "wężyk" cyli wykres i masz" sorry ale nie wiem
o czym mówisz

30 wrz 23:14
Czarek1994: aha

dzięki

30 wrz 23:14
Czarek1994: x2 ≥ −9 sprzeczność tak ?
30 wrz 23:17
krystek: a dlaczego?
30 wrz 23:19
krystek: prawdziwe dla każdego x
X2+9≥0
30 wrz 23:21
Czarek1994: No (x+3)2 = x2 + 9 ≥ 0 i przenoszę i mam x2 ≥ 9
a przecież nic podniesione do kwadratu nie może być ujemne
30 wrz 23:22
krystek: Oj wzory skróconego mnożenia się kłaniają!
30 wrz 23:23
Czarek1994: No dobrze już rozumiem ale dlaczego wykres ma −3 i 3 ?
30 wrz 23:24
Czarek1994: O kurcze no tak ... racje przepraszam za zawracanie głowy x
2 + 6x +9

30 wrz 23:25
krystek: Poźna pora idź spać, na lekcji nie będziesz myślał.
30 wrz 23:27
Czarek1994: Dam radę mam nadzieje

nie mogę dostać bani już jedną mam z planimetrii

za trudny dział
jak dla mnie ta planimetria a ta strona mimo, że taka fajna o planimetrii ma zbyt mało

30 wrz 23:30
krystek: Jest mnóstwo zadań ,wyszukaj !
30 wrz 23:32
krystek: Masz u góry "szukaj na forum"
30 wrz 23:33
Czarek1994: To wiem jestem tu od 2 lat regularnie dzięki tej stronie ze sprawdzianu całorocznego z matmy w
1 klasie technikum dostałem 4+ a miałem 2 na półrocze także mogę śmiało powiedzieć, że się
staram
30 wrz 23:38
Czarek1994: No dobra ostatnia próba na dziś dlaczego wykres wygląda tak jak wygląda tzn. do −3 spada do −2
parabola nad osią do 2 pod osią i do 3 nad osią ?
30 wrz 23:45
30 wrz 23:48
Gustlik: Krystku, ale na maturze Horner znacznie skraca rozwiązywanie tego typu zadań, dlatego
trzeba go znać. A krótsza metoda = krótszy czas rozwiązywania zadań = więcej punktów = lepszy
wynik matury = większa szansa na upragniony kierunek studiów. Pamiętaj, że CKE da tyle samo
punktów za wielomian rozwiązany Hornerem co za ten sam wielomian rozwiązany w inny sposób, np.
grupowaniem, a wiec robiąc dłuższą metodą maturzysta nic nie zyska w takim zadaniu, a tylko
straci cenny czas. Owszem − grupowanie też dobra rzecz, ale w ramach zabawy w domu, jako
gimnastyka mózgu.
30 wrz 23:58
aaaaaaaaaaaaaaaa: a
1 paź 18:07
 "pod ten" x= −1 , czyli "pod"
dwumian (x+1) np. tak :
x3−4x2+x+6=0 ⇔ x3+x2 −5x2−5x +6x+6= 0 ⇔ x2(x+1)−5x(x+1)+6(x+1)= 0 ⇔
⇔ (x+1)(x2−5x+6)= 0 i np. ze wzorów Viete'a ⇔ (x+1)(x−2)(x−3)= 0 ⇔ x∊{2,−1,3} .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
4) x ≥1x /* x2 >0 i x≠0 ⇒ x3 ≥x ⇔ x3−x ≥0 ⇔ x(x2−1) ≥0 ⇔
⇔ x(x−1)(x+1) ≥ 0 i x≠0 ⇔ x∊<−1;0) U <1;+∞) . ...
"pod ten" x= −1 , czyli "pod"
dwumian (x+1) np. tak :
x3−4x2+x+6=0 ⇔ x3+x2 −5x2−5x +6x+6= 0 ⇔ x2(x+1)−5x(x+1)+6(x+1)= 0 ⇔
⇔ (x+1)(x2−5x+6)= 0 i np. ze wzorów Viete'a ⇔ (x+1)(x−2)(x−3)= 0 ⇔ x∊{2,−1,3} .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
4) x ≥1x /* x2 >0 i x≠0 ⇒ x3 ≥x ⇔ x3−x ≥0 ⇔ x(x2−1) ≥0 ⇔
⇔ x(x−1)(x+1) ≥ 0 i x≠0 ⇔ x∊<−1;0) U <1;+∞) . ... 

 jeśli mam tak robić to wypadało by coś na ten
temat wiedzieć
jeśli mam tak robić to wypadało by coś na ten
temat wiedzieć 




 dzięki
dzięki 

 nie mogę dostać bani już jedną mam z planimetrii
nie mogę dostać bani już jedną mam z planimetrii za trudny dział
jak dla mnie ta planimetria a ta strona mimo, że taka fajna o planimetrii ma zbyt mało
za trudny dział
jak dla mnie ta planimetria a ta strona mimo, że taka fajna o planimetrii ma zbyt mało