Rozwiąż nierówność:
Adrian: Rozwiąż nierówność:
x3+6x2+11x+6>0
27 wrz 21:59
Saizou : w(−1)=−1+6−11+6=0
i podziel przez x+1
27 wrz 22:00
ICSP: w(−1) = 0 zatem możesz podzielić ten wielomian przez dwumian (x+1)
27 wrz 22:01
Saizou : byłem szybszy
27 wrz 22:02
ICSP: pff
27 wrz 22:02
Adrian: Dziękuję Bardzo za pomoc. na śmierć zapomniałem o twierdzeniu bezout
27 wrz 22:03
ICSP: a podzielić w pamięci i wyznaczyć pozostałe pierwiastki potrafisz ?
27 wrz 22:03
Adrian: w pamięci ciężko
27 wrz 22:04
Saizou : dzisiaj na lekcji ten przykład miałem
27 wrz 22:05
Saizou : znaczy się chodzi mi poźniej o funkcję kwadratową
27 wrz 22:05
Adrian: ja staram się zaprzyjaźnić z Panem Kiełbasą
27 wrz 22:05
Adrian: z resztą sobie dam radę
27 wrz 22:06
Saizou : "smacznego" jutro jest piątek
27 wrz 22:06
Adrian: będę pościł
27 wrz 22:06
Saizou : o widzę że kolego też w 2 LO na R
27 wrz 22:07
Adrian: jestem w IV tech
27 wrz 22:08
Saizou : powtórki?
27 wrz 22:08
ICSP: to patrz
Saizou na to :
w(x) = x
3 + 6x
2 + 11x + 6 = x
3 + x
2 +
5x
2 + 11x +
6 = (x+1)(x
2 +
5x +
6)i teraz mam że suma dwóch pozostałych pierwiastków to −5 a ich iloczyn to 6. W takim
razie x
2 = −2 oraz x
3 = −3
w(x) = (x+1)(x+2)(x+3)
tak właśnie rozkładam wielomiany w pamięci na szybko
Oczywiście czasem się pomylę ale zazwyczaj działa
27 wrz 22:09
Adrian: niee, nawet tego wcześniej nie miałem
jakiś czas temu stwierdziłem, że chce napisać
rozszerzenie
27 wrz 22:10
Saizou : bardzo ciekawy sposób
27 wrz 22:11
Adrian: w zasadzie miałbym jeszcze jedno pytanie
27 wrz 22:12
Adrian: jak mam funkcję kwadratową to w jakich sytuacjach pierwiastek jest parzysty, a w jakich nie?
27 wrz 22:13
ICSP: pierwiastek parzysty ?
Coż to takiego ?
27 wrz 22:14
Saizou : ja się jeszcze nie spotkałem z metodą przewidywania czy pierwiastek jest parzysty, zawsze
liczyłem Δ i pierwiastki (no nie zawsze)
27 wrz 22:15
Saizou : ja potraktowałem to jako liczbę parzystą, która jest pierwiastkiem
27 wrz 22:16
27 wrz 22:16
Adrian: znaczyy chodzi mi o krotność
27 wrz 22:16
ICSP: Δ = 0 − pierwiastek dwukrotny
Δ > 0 − dwa pierwiastki jednokrotne
Δ < 0 − wiadomo
27 wrz 22:17
Saizou : jeśli Δ=0 to masz pierwiastek dwukrotny (bo idzie wtedy zwinąć to wyrażenia za pomocą wzoru)
jeśli Δ=0 pierwiastki są jednokrotne
27 wrz 22:17
Saizou : znaczy się Δ>0 to są jednokrotne
27 wrz 22:18
Adrian: to pomóżcie mi jeszcze w tej nierówności
−x3+x2+x−1≥0
27 wrz 22:21
ICSP: od razu widać grupowanie :
−x3 + x2 + x − 1 ≥ 0
x3 − x2 − x + 1 ≤ 0
x2(x−1) − 1(x−1) ≤ 0
(x−1)2(x+1) ≤ 0
27 wrz 22:23
Adrian:
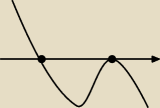
i nie wiem dlaczego mam taki wykres
27 wrz 22:27
Adrian: czemu oś od x=1 sie odbija
27 wrz 22:28
ICSP: ponieważ x = 1 jest pierwiastkiem dwukrotnym. Wykres odbija się od Osi dla pierwiastków
parzystych krotności.
27 wrz 22:29
Adrian: masakra, jaki ze mnie idiota....
27 wrz 22:29
27 wrz 22:31
Adrian: no dobra, ale rozwiązanie jest takie:
x∊ (−∞;−1) u {1}
27 wrz 22:34
Adrian: x∊ (−∞;−1> u {1}
27 wrz 22:34
Aga1.: (x−1)2(x+1)≤0⇔x∊<−1,∞)
29 wrz 10:48
Basia:
(x−1)2 ≥ 0 dla każdego x∊R
(x−1)2(x+1) ≤ 0 ⇔ x−1=0 lub x+1≤0 ⇔ x=1 lub x≤ −1 ⇔ x∊(−∞;−1>∪{1}
odpowiedź podana przez Adriana jest poprawna
29 wrz 10:54
Beata: −2x4−4x3+6x2≤0
9 kwi 16:57
Beata: x3−3x2−4x+12>0
9 kwi 17:02